class-vi-math-chapter-1.2 - LET US LEARN MATHEMATICS

এই পোস্ট টি তে আমরা ষষ্ঠ শ্রেণীর গনিত প্রভা (Gonit Prabha-vi) বই এর কষেদেখি- ১.২ ( কষেদেখি -1.2)এর সকল সমস্যার সমাধান (Mathematics solution) সহজ ভাবে করেছি যা তোমাদের অনেক ভালো ভাবে বুঝতে সাহায্য করবে, WB-গনিত-প্রভা-ষষ্ঠ-শ্রেণী (Class-VI)-কষেদেখি -1.(পূর্বপাঠের পুনরালোচনা), WB-class-vi-kosedekhi-1.2, WB-math-class-vi-kosedekhi-1.2, WB-math-class-6-kosedekhi-1.2,

কষে দেখি-1.2

1.মনে মনে করিঃ

a. শুন্য ছাড়া 5 -এর 6 টি গুনিতক খুঁজি

সমাধানঃ শুন্য ছাড়া 5 -এর 6 টি গুনিতক হল –5, 10, 15, 20, 25, 35,….

b. 7 এর 3 টি গুনিতক খুঁজি যারা 50 এর থেকে বড়ো ।

সমাধানঃ 7 এর 3 টি গুনিতক যারা 50 এর থেকে বড়ো সেগুলি হলঃ 56, 63,70

c. দুটি 2 অঙ্কের সংখ্যা ভাবি যারা 4 এর গুনিতক।

সমাধানঃ দুটি 2 অঙ্কের সংখ্যা যারা 4 এর গুনিতক তা হল –12, 16.

d. 4 কোন কোন সংখ্যার উৎপাদক বা গুণনীয়ক হতে পারে এমন তিনটি সংখ্যা লিখি।

সমাধানঃ 4 উৎপাদক বা গুণনীয়ক হতে পারে এমন তিনটি সংখ্যা —12, 16, 20.

e. এমন দুটি সংখ্যা খুঁজি যাদের ল. সা. গু. 12 ও যোগফল 10

সমাধানঃ

a. $(1 \, 9) \Rightarrow 1+9=10$ এবং লসাগু = 9,

b. $(2 \, 8) \Rightarrow 2+8=10$ এবং লসাগু = 8,

c. $(3 \, 7) \Rightarrow 3+7=10$ এবং লসাগু = 21,

d. $(4 \, 6) \Rightarrow 4+6=10$

এবং লসাগু = 12,

e. $(5 \, 5) \Rightarrow 5+5=10$ এবং লসাগু = 5,

দুটি সংখ্যা যাদের ল. সা. গু. 12 ও যোগফল 10 তারা হলঃ 4, এবং 6

2. (a). 14 এর মৌলিক উৎপাদক গুলি কি কি ?

সমাধানঃ

$14=1 \times 2 \times 7$

$\therefore$ 14 এর মৌলিক উৎপাদক গুলি হলঃ 2, 7 (1 এর ক্ষেত্রে উৎপাদক দুটি আলাদা নয়, তাই 1 মৌলিক নয় আবার যৌগিকও নয় )

(b). সব থেকে ছোট মৌলিক সংখ্যা কি?

সমাধানঃ সবথেকে ছোট মৌলিক সংখ্যা = 2

(c). কোন সংখ্যা মৌলিক ও নয় আবার যৌগিক ও নয়

সমাধানঃ 1 কারন 1 এর ক্ষেত্রে উৎপাদক দুটি আলাদা নয়, তাই 1 মৌলিক নয় আবার যৌগিকও নয় ।

3. (A). 42 কোন কোন সংখ্যার গুনিতক —-(a). 7 (b). 13 (c). 5 (d). 6

সমাধানঃ যেকোনো সংখ্যাকে সবসময়ে তার যে কোনও উৎপাদকের গুনিতক আকারে প্রকাশ করা যায়।

$\therefore$

42 কোন কোন সংখ্যার গুনিতক, অন্য ভাবে বললে হয় 42 তার কোন কোন উৎপাদক গুলির গুনিতক …

$42= 1 \times 2 \times 3 \times 7$

$\therefore$ 42 কোন কোন সংখ্যার গুনিতক তাহলোঃ (a). 7 (d). 6

(B). 11 কোন সংখ্যার গুণনীয়ক—- (a). 101 (b). 111 (c). 121 (d). 112

সমাধানঃ

11 কোন সংখ্যার গুণনীয়ক এর মানে উপরের কোন সংখ্যা গুলি 11 এর গুনিতক খুঁজলে আমারা উত্তর টি পেয়ে যাব

$101= 1 \times 101\\\\ 111=3 \times 37\\\\ 121=11 \times 11\\\\112= 2 \times 2 \times 2 \times 2 \times 7$

$\therefore$ 11 , (c). 121 এর গুণনীয়ক ।

4. সংখ্যা জোড়ার মধ্যে কোনগুলি পরস্পর মৌলিক সংখ্যা দেখিঃ

$\bigstar$ পরস্পর মৌলিক সংখ্যা কাকে বলে ?

CLASS-VI-দাগ নাম্বার -5 & 6-Annual Examination—2021/MODEL QUESTION solved /Mathematics

দুটি সংখ্যাকে পরস্পর মৌলিক সংখ্যা বলা হবে যদি তাদের মধ্যে 1 ছাড়া আর অন্য কোন সাধারন উৎপাদক না থাকে ।

অন্য ভাবে বলা যায়, দুটি সংখ্যার গসাগু যদি 1 হয় তাহলে সংখ্যা দুটি পরস্পর মৌলিক সংখ্যা ।

(a). 5, 7

সমাধানঃ পরস্পর মৌলিক সংখ্যা

(b). 10, 21

সমাধানঃ

$10=1 \times 2 \times 5\\\\ 21= 1 \times 3 \times 7$

10, 21 এর গসাগু = 1

$\therefore$ 10, 21 পরস্পর মৌলিক সংখ্যা ।

(c). 10, 15

সমাধানঃ

$10 = 1 \times 2 \times 5 \\\\ 15 = 1 \times 3 \times 5$

$\therefore$ 10, 15 এর গসাগু = 5

$\therefore$ 10, 15 পরস্পর মৌলিক সংখ্যা নয় ।

(d). 16, 15

সমাধানঃ

$16 = 1 \times 2 \times 2 \times 2 \times 2 \\\\ 15 = 1 \times 3 \times 5$

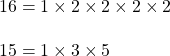
$\therefore$ 16, 15 এর গসাগু = 1

$\therefore$ 16, 15 পরস্পর মৌলিক সংখ্যা ।

5. এমন দুটি যৌগিক সংখ্যা খুজি যারা পরস্পর মৌলিক ?

সমাধানঃ

$\bigstar$ যৌগিক সংখ্যা কাকে বলে?

$\Rightarrow$ কোন সংখ্যার যদি 1 এবং সেই সংখ্যা ছাড়াও অন্য উৎপাদক থাকে তাকে যৌগিক সংখ্যা বলে ।

$15= 1 \times 3 \times 5\\\\ 16 = 1 \times 2 \times 2 \times 2 \times 2$

15, 16 নিজেরা যৌগিক সংখ্যা কিন্তু পরস্পর মৌলিক সংখ্যা ।

$15 = 1 \times 3 \times 5 \\\\ 22= 1 \times 2 \times 11$

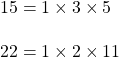
15, 22 নিজেরা যৌগিক সংখ্যা কিন্তু পরস্পর মৌলিক সংখ্যা ।

6. (a). পরস্পর মৌলিক সংখ্যার গসাগু কত?

সমাধানঃ

পরস্পর মৌলিক সংখ্যার মধ্যে একমাত্র সাধারন উৎপাদক হল ১ ।

$\therefore$ পরস্পর মৌলিক সংখ্যার গসাগু ১।

(b). পরস্পর মৌলিক সংখ্যার লসাগু কত লিখি?

সমাধানঃ

আমরা জানি, কোন দুটি সংখ্যার গসাগু $\times$ লসাগু = সংখ্যা দুটির গুনফল

পরস্পর মৌলিক সংখ্যার গসাগু = 1

$\therefore$ পরস্পর মৌলিক সংখ্যার লসাগু= সংখ্যা দুটির গুনফল ।

7. নীচের সংখ্যা গুলি 1 এবং মৌলিক উৎপাদকে বিশ্লেষণ করে গসাগু খুঁজি —–

(a). 22 , 44

সমাধানঃ

$22 = 1\times 2 \times 11$

$44 = 1 \times 2 \times 2 \times 11$

$\therefore$ 22 , 44 এর গসাগু = $1 \times 2 \times 11=22$

(b). 54, 72

সমাধানঃ

$54= 1 \times 2 \times 3 \times 3 \times 3$

$72 = 1 \times 2 \times 2 \times 2 \times 3 \times 3$

$\therefore$ 54 , 72 এর গসাগু = $1 \times 2 \times 3 \times 3= 18$

(c). 27, 64

সমাধানঃ

$27= 1 \times 3 \times 3 \times 3$

$64 = 1 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$

$\therefore$ 27 , 64 এর গসাগু = 1

(d). 36, 30

সমাধানঃ

$36= 1 \times 2 \times 2 \times 3 \times 3$

$30 = 1 \times 2 \times 3 \times 5$

$\therefore$ 36 , 30 এর গসাগু = $1 \times 2 \times 3 =6$

(e). 28, 35, 49

সমাধানঃ

$28= 1 \times 2 \times 2 \times 7$

$35 = 1 \times 5 \times 7$

$49 = 1 \times 7 \times 7$

$\therefore$ 28 , 35, 49 এর গসাগু = $1 \times 7 = 7$

(f). 30, 72, 96

সমাধানঃ

$30 = 1 \times 2 \times 3 \times 5$

$72 = 1 \times 2 \times 2 \times 2 \times 3 \times 3$

$96 = 1 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3$

$\therefore$ 30, 72, 96 এর গসাগু = $1 \times 2 \times 3 = 6$

(g). 20,

8. সংখ্যাগুলির ভাগ পদ্ধতিতে গসাগু খুঁজি——-

(a). 28, 35

সমাধানঃ

সমাধানঃ

সমাধানঃ

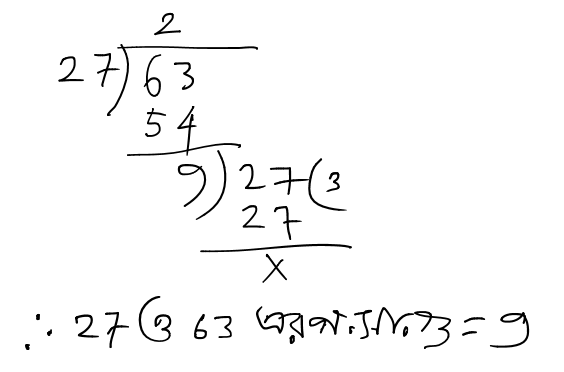
(d). 25, 35, 45

সমাধানঃ

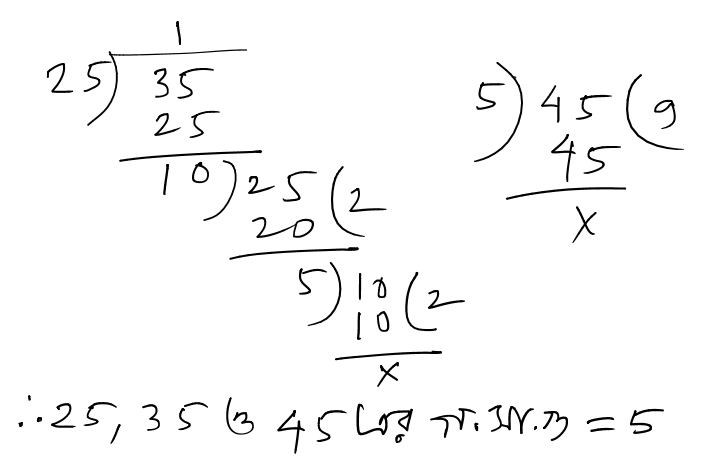
(e). 48, 72, 96

সমাধানঃ

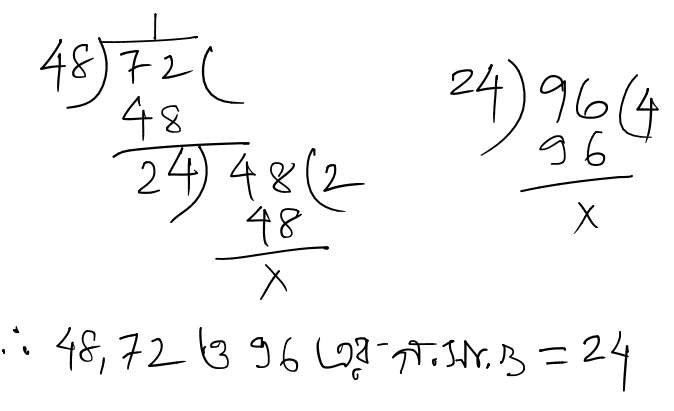
9. নীচের সংখ্যাগুলি মৌলিক উৎপাদকে বিশ্লেষণ করে লসাগু খুঁজি ———

(a). 25, 80

সমাধানঃ

$25 = 1 \times 5 \times 5$

$80 = 1 \times 2 \times 2 \times 2 \times 2 \times 5$

$\therefore$ 25, 80 এর লসাগু = $1 \times 5 \times 5 \times 2 \times 2 \times 2 \times 2 =400$

(b). 36, 39

সমাধানঃ

$36 = 1 \times 2 \times 2 \times 3 \times 3$

$39 = 1 \times 3 \times 13$

$\therefore$ 36, 39 এর লসাগু = $1 \times 2 \times 2 \times 3 \times 3 \times 13 = 468$

(c). 32, 56

সমাধানঃ

$32 = 1 \times 2 \times 2 \times 2 \times 2 \times 2$

$56 = 1 \times 2 \times 2 \times 2 \times 7$

$\therefore$ 32, 56 এর লসাগু = $1 \times 2 \times 2 \times 2 \times 2 \times 2 \times 7 = 224$

(d). 36, 48, 72

সমাধানঃ

$36 = 1 \times 2 \times 2 \times 3 \times 3$

$48 = 1 \times 2 \times 2 \times 2 \times 2 \times 3$

$72 = 1 \times 2 \times 2 \times 2 \times 3 \times 3$

$\therefore$ 36, 48, 72 এর লসাগু = $1 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 = 144$

(e). 25, 35, 45

সমাধানঃ

$25 = 1 \times 5 \times 5$

$35 = 1 \times 5 \times 7$

$45 = 1 \times 3 \times 3 \times 5$

$\therefore$ 36, 48, 72 এর লসাগু = $1 \times 3 \times 3 \times 5 \times 5 \times 7 = 1575$

(f). 32, 40 , 84

সমাধানঃ

$32 = 1 \times 2 \times 2 \times 2 \times 2 \times 2$

$40 = 1 \times 2 \times 2 \times 2 \times 5$

$84 = 1 \times 2 \times 2 \times 3 \times 7$

$\therefore$ 32, 40, 84 এর লসাগু = $1 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 5 \times 7 = 3360$

10. সংখ্যা জোড়ের মধ্যে কোনগুলি পরস্পর মৌলিক ——

(a). 47, 23

সমাধানঃ

দুটি সংখ্যার গসাগু যদি 1 হয় তাহলে সংখ্যা দুটি পরস্পর মৌলিক সংখ্যা ।

class-vi-math-chapter-1.1

$47= 1 \times 47$

$23 = 1 \times 23$

$\therefore$ 47, 23, এর গসাগু = $1$

$\therefore$ সংখ্যা দুটি পরস্পর মৌলিক ।

(b). 25, 9

সমাধানঃ

দুটি সংখ্যার গসাগু যদি 1 হয় তাহলে সংখ্যা দুটি পরস্পর মৌলিক সংখ্যা ।

$25= 1 \times 5 \times 5$

$9 = 1 \times 3 \times 3$

$\therefore$ 25, 9, এর গসাগু = $1$

$\therefore$ সংখ্যা দুটি পরস্পর মৌলিক ।

(c). 49, 35

সমাধানঃ

দুটি সংখ্যার গসাগু যদি 1 হয় তাহলে সংখ্যা দুটি পরস্পর মৌলিক সংখ্যা ।

$49= 1 \times 7 \times 7$

$35 = 1 \times 5 \times 7$

$\therefore$ 49, 35, এর গসাগু = $1 \times 7=7$

$\therefore$ সংখ্যা দুটি পরস্পর মৌলিক নয় ।

(d). 36, 54

সমাধানঃ

দুটি সংখ্যার গসাগু যদি 1 হয় তাহলে সংখ্যা দুটি পরস্পর মৌলিক সংখ্যা ।

$36= 1 \times 2 \times 2 \times 3 \times 3$

$54 = 1 \times 2 \times 3 \times 3 \times 3$

$\therefore$ 36, 54, এর গসাগু = $1 \times 2 \times 3 \times 3 =18$

$\therefore$ সংখ্যা দুটি পরস্পর মৌলিক নয় ।

11. সংক্ষিপ্ত ভাগ পদ্ধতিতে নীচের সংখ্যাগুলির গসাগু ও লসাগু নির্ণয় করো ——

(a). 33 এবং 132

সমাধানঃ

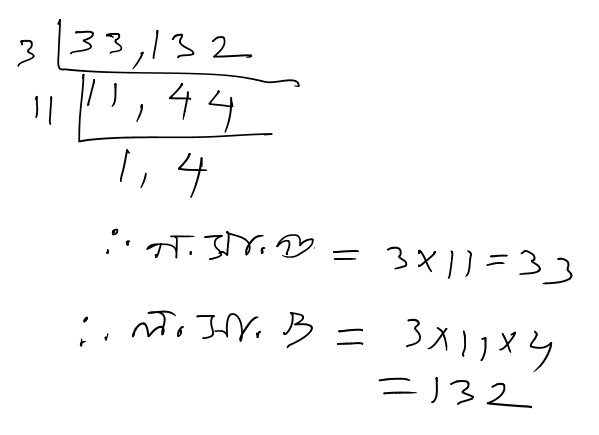
(b). 90 এবং 144

সমাধানঃ

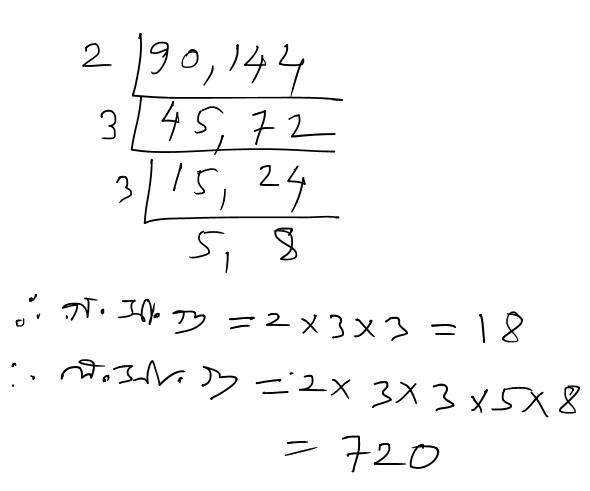
(c). 32, 40 এবং 72

সমাধানঃ

(d). 28, 49 এবং 70

সমাধানঃ

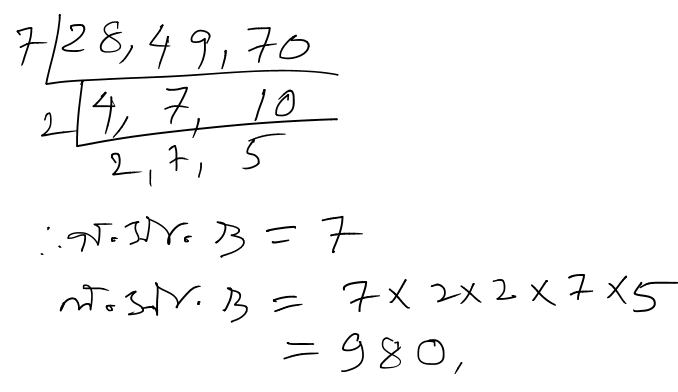
12. সব থকে ছোট সংখ্যা খুঁজি যা 18, 24 ও 42 দিয়ে বিভাজ্য।

সমাধানঃ

সব থেকে ছোট সংখ্যা যা 18, 24 , 42 দিয়ে বিভাজ্য তা হল 18, 24 ও 42 এর লসাগু

$\therefore$ সবথেকে ছোট সংখ্যা হল 504 যা 18, 24 ও 42 দিয়ে বিভাজ্য।

13. সবচেয়ে বড়ো সংখ্যা খুঁজি যা দিয়ে 45 ও 60 কে ভাগ করলে কোনো ভাগশেষ থাকবে না ।

সমাধানঃ

সবচেয়ে বড়ো সংখ্যা যা দিয়ে 45 ও 60 কে ভাগ করলে কোনো ভাগশেষ থাকবে না তা হল 45 ও 60 এর গসাগু

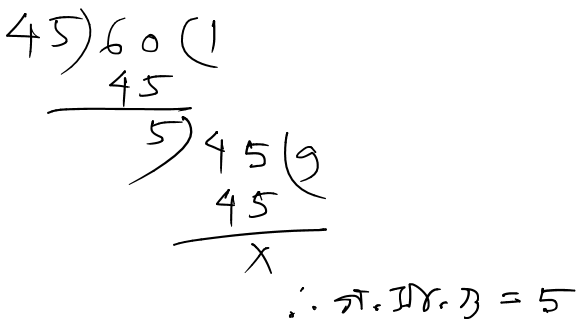
$\therefore$ সবচেয়ে বড়ো সংখ্যা হল 5 যা দিয়ে 45 ও 60 কে ভাগ করলে কোনো ভাগশেষ থাকবে না ।

14. দুটি সংখ্যার লসাগু ও গসাগু যথাক্রমে 252 ও 6 ; সংখ্যা দুটির গুনফল কত হিসাব করি ।

সমাধানঃ

আমরা জানি যে, সংখ্যা দুটির গুনফল = সংখ্যা দুটির লসাগু $\times$ গাসগু

$\therefore$ সংখ্যা দুটির গুনফল $= 252 \times 6$

$\Rightarrow$ সংখ্যা দুটির গুনফল $= 1512$

15. দুটি সংখ্যার গসাগু ও লসাগু যথাক্রমে 8 ও 280 ; একটি সংখ্যা 56 হলে অপর সংখ্যাটি কত হিসাব করি ।

সমাধানঃ

আমরা জানি যে, সংখ্যা দুটির গুনফল = সংখ্যা দুটির লসাগু $\times$ গাসগু

$\Rightarrow 56 \times$ অপর সংখ্যা $= 280 \times 8$

$\Rightarrow$ অপর সংখ্যা = $\frac{280 \times 8}{56} = 40$

16. দুটি সংখ্যার গসাগু 1 ; সংখ্যা দুটি লিখি ।

সমাধানঃ

দুটি সংখ্যার গসাগু =1, অর্থাৎ সংখ্যা দুটি পরস্পর মৌলিক

যেমন – 14 ও 15 ; 14 ও 19 ইতাদি

17. 48 টি রসগোল্লা ও 64 টি সন্দেশ কোনটি না ভেঙ্গে সবচেয়ে বেশি কতজনকে সমান সংখ্যায় দেওয়া যাবে দেখি ।

সমাধানঃ

48 টি রসগোল্লা ও 64 টি সন্দেশ কোনটি না ভেঙ্গে সবচেয়ে বেশি কতজনকে সমান সংখ্যায় দেওয়া যাবে তা হল 48 ও 64 এর গসাগু

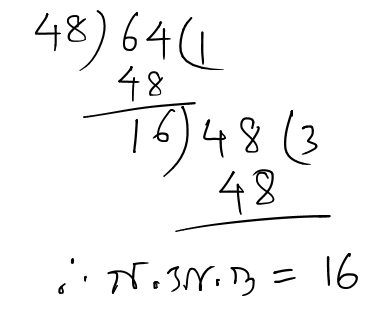
Model-Activity-Task-VI-Mathematics

$\therefore$ 48 টি রসগোল্লা ও 64 টি সন্দেশ কোনটি না ভেঙ্গে সবচেয়ে বেশি 16 জনকে সমান সংখ্যায় দেওয়া যাবে ।

18. বিভাস ও তার বন্ধুরা মিলে 8 জন অথবা 10 জন করে সদস্য নিয়ে নাটকের একটি দল তৈরির কথা ভাবল । কমপক্ষে কতজন থাকলে উভয় প্রকার দল তৈরি করতে পারবে হিসাব করি ।

সমাধানঃ

বিভাস ও তার বন্ধুরা মিলে 8 জন অথবা 10 জন করে সদস্য নিয়ে নাটকের একটি দল তৈরির কথা ভাবল । কমপক্ষে কতজন থাকলে উভয় প্রকার দল তৈরি করতে পারবে তা হল 8 ও 10 এর লসাগু

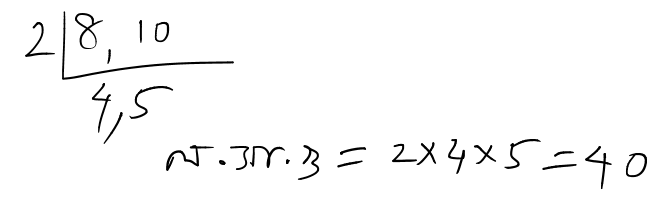
$\therefore$ কমপক্ষে 40 জন থাকলে উভয় প্রকার দল তৈরি করতে পারবে ।

19. যদুনাথ বিদ্যামন্দির স্কুলের ষষ্ঠ শ্রেণীর ছাত্রছাত্রীদের স্কুলের বাগানে ফুলের চারা লাগানোর জন্যে পঞ্চায়েত থেকে ফুলের চারা পাঠিয়েছে । হিসাব করে দেখা গেল চারাগুলিকে 20 টি, 24 টি, বা 30 টি সারিতে লাগালে প্রতিক্ষেত্রে প্রতিসারিতে সমান চারা থাকে । পঞ্চায়েত থেকে কমপক্ষে কতগুলি চারা পাঠিয়েছিল হিসাব করে দেখি ।

সমাধানঃ

যেহেতু চারাগুলিকে 20 টি, 24 টি, বা 30 টি সারিতে লাগালে প্রতিক্ষেত্রে প্রতিসারিতে সমান চারা থাকে অর্থাৎ মোট চারার সংখ্যা 20, 24, 30 দিয়ে বিভাজ্য ,

20, 24, 30 দিয়ে বিভাজ্য সব থেকে ছোট সংখ্যা হল, 20, 24, 30 এর লসাগু

$\therefore$ পঞ্চায়েত থেকে কমপক্ষে কতগুলি চারা পাঠিয়েছিল তা হল 20, 24, 30 এর লসাগু

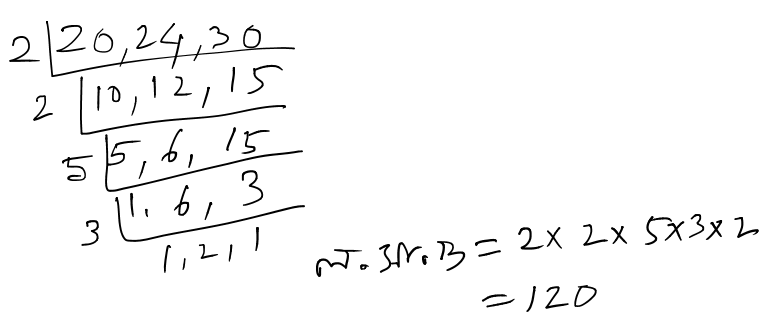
$\therefore$ $\therefore$ পঞ্চায়েত থেকে কমপক্ষে 120 টি চারা পাঠিয়েছিল ।

20. একটি ইঞ্জিনের সামনের চাকার পরিধি 14 ডেসিমি এবং পিছনের চাকার পরিধি 35 ডেসিমি । কমপক্ষে কত পথ গেলে চাকা দুটি একই সঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে হিসাব করি ।

সমাধানঃ

ইঞ্জিনের সামনের চাকার পরিধি 14 ডেসিমি এবং পিছনের চাকার পরিধি 35 ডেসিমি,
কমপক্ষে কত পথ গেলে চাকা দুটি একেই সঙ্গে পূর্ন্যসংখ্যক বার ঘুরবে তার মানে নুন্যতম কোন দূরত্ব 14 ও 35 দিয়ে ভিভাজ্য,

নুন্যতম সেই দূরত্ব হলো 14 ও 35 এর ল. সা. গু.

$\therefore$ কমপক্ষে 70 ডেসিমি পথ গেলে চাকা দুটি একেই সঙ্গে পূর্ন্যসংখ্যক বার
ঘুরবে।

21. আমি প্রতিক্ষেত্রে দুটি করে সংখ্যা লিখি যাদের

(a). গসাগু 7

সমাধানঃ

দুটি সংখ্যা যাদের গসাগু 7 এমন দুটি সংখ্যা হল : 7 ও 21

(b). লসাগু 12

সমাধানঃ

দুটি সংখ্যা যাদের লসাগু 12 এমন দুটি সংখ্যা হল: 3 ও 4

(c).

এই সমাধান গুলোর ভিডিও লিঙ্কঃ https://www.youtube.com/watch?v=4uT6jeBgz64&t=172s

Spread/ share this post

কষে দেখি-1.2

8. সংখ্যাগুলির ভাগ পদ্ধতিতে গসাগু খুঁজি——-

Leave a Comment Cancel reply