1. ![]() বহুপদী সংখ্যামালার
বহুপদী সংখ্যামালার ![]() এর সহগ কত নির্ণয় করো
এর সহগ কত নির্ণয় করো
a). ![]()
b). ![]()
c). ![]()
d). ![]()
উত্তরঃ

![]()

![]() b).
b). ![]() সঠিক
সঠিক
2. ![]() এর মান নির্ণয় করো
এর মান নির্ণয় করো
a). ![]()
b). ![]()
c). ![]()
d). ![]()
উত্তরঃ

সঠিক উত্তরঃ d). ![]()
3. ![]() এর
এর ![]() % +
% + ![]() এর
এর ![]() %
% ![]() এর
এর ![]() %
%
a). ![]()
b). ![]()
c). ![]()
d). কোনোটি নয়
উত্তরঃ
![]() এর
এর ![]() % +
% + ![]() এর
এর ![]() %
% ![]() এর
এর ![]() %
% 
![]()
সঠিক উত্তরঃ b). ![]()
4. ![]() এর
এর ![]() % এর
% এর ![]() এর
এর ![]()
a). 18
b). 21
c). 19
d). 28
উত্তরঃ
![]() এর
এর ![]() % এর
% এর ![]() এর
এর ![]()

![]() c). 19 সঠিক
c). 19 সঠিক
5. ![]() হলে
হলে ![]() এর মান কত ?
এর মান কত ?
উত্তরঃ
![]()
(i) নং এর উভয়পক্ষকে বর্গ করে পাই, 
![]()
(i) নং এর উভয়পক্ষকে ঘন করে পাই, 
![]()
![]() নং ও
নং ও ![]() নং কে গুন করে পাই,
নং কে গুন করে পাই, 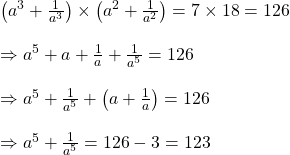
![]()
6. ![]() হলে
হলে ![]() কত হবে ?
কত হবে ?
উত্তরঃ
![]()
![]() এর উভয়পক্ষকে
এর উভয়পক্ষকে ![]() দিয়ে গুন করে পাই,
দিয়ে গুন করে পাই, 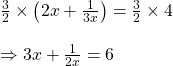
![]()
![]() নং এর উভয়পক্ষকে ঘন করে পাই,
নং এর উভয়পক্ষকে ঘন করে পাই, 
![]()
7. ![]() হলে
হলে ![]() এর মান কত হবে?
এর মান কত হবে?
উত্তরঃ
![]()
(i) নম্বরের উভয়পক্ষকে 3 দিন গুন করে পাই , ![]()
(iii) নং এর উভয়পক্ষকে ঘন করে পাই,
![]()
8. প্রথম 100 যুগ্ম সংখ্যার যোগফল। …….
a). 100 দিয়ে বিভাজ্য কিন্তু 101 দিয়ে বিভাজ্য নয়
b). 101 দিয়ে বিভাজ্য কিন্তু 100 বিভাজ্য নয়
c).100 এবং 101 দিয়ে বিভাজ্য
d). 100 বা 101 কোনটি দিয়ে বিভাজ্য নয়
উত্তরঃ
প্রথম 100 যুগ্ম সংখ্যাগুলি হলো : 2, 4, 6, 8,…, 200.
প্রথম 100 যুগ্ম সংখ্যার যোগফল =

![]() n সংখ্যক স্বাভাবিক সংখ্যার যোগফল :
n সংখ্যক স্বাভাবিক সংখ্যার যোগফল :
![]()
![]() প্রথম 100 যুগ্ম সংখ্যার যোগফল = 100 × 101
প্রথম 100 যুগ্ম সংখ্যার যোগফল = 100 × 101
c).100 এবং 101 দিয়ে বিভাজ্য (সঠিক )
9.  এর সবচেয়ে ছোটো কোন মানের জন্যে
এর সবচেয়ে ছোটো কোন মানের জন্যে 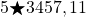 দিয়ে বিভাজ্য হবে।
দিয়ে বিভাজ্য হবে।
কোনো সংখ্যা 11 দিয়ে বিভাজ্য কিনা চেক করার নিয়ম হলো :
সংখ্যাটির অযুগ্ম স্থানের অঙ্কের যোগফলের থেকে যুগ্ম স্থানের অঙ্কগুলির যোগফল বিয়োগ
করলে যদি বিয়োগফল 0 অথবা 11 এর গুণিতক হয়, তাহলে সংখ্যাটি 11 দিয়ে বিভাজ্য। ![]() সংখ্যাটির অযুগ্ম স্থানের অঙ্কগুলির যোগফল
সংখ্যাটির অযুগ্ম স্থানের অঙ্কগুলির যোগফল ![]()
এবং সংখ্যাটির যুগ্ম স্থানের অঙ্কগুলির যোগফল ![]()
সবথেকে ছোটো যে মানের জন্যে সংখ্যাটি 11 দিয়ে বিভাজ্য তাহলো 
1. যদি 7 টি বিড়াল 7 টি ইঁদুর খেতে 7 মিনিট সময় নেয়, তাহলে 1000 টি বিড়াল 1000 টি ইঁদুর খেতে
কত সময় নেবে ?
উত্তরঃ
7 টি বেড়াল 7 টি ইঁদুর খেতে 7 মিনিট সময় নেয়
1 টি বেড়াল 7 টি ইঁদুর খেতে 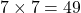 মিনিট সময় নেবে
মিনিট সময় নেবে
1 টি বেড়াল 1 টি ইঁদুর খেতে সময় নেবে  মিনিট
মিনিট
1000 টি বেড়াল 1 টি ইঁদুর খেতে সময় নেবে  মিনিট
মিনিট
1000 টি বেড়াল 1000 টি ইঁদুর খেতে সময় নেবে  মিনিট
মিনিট
 1000 টি বিড়াল 1000 টি ইঁদুর খেতে 7 মিনিট সময় নেবে
1000 টি বিড়াল 1000 টি ইঁদুর খেতে 7 মিনিট সময় নেবে
competitive exams:
http://sdtutoronline.com/competitive-exams/
আরও উন্নিতির জন্যে সকলের কাছে থেকে যেকোনো পরামর্শ সাদরে গ্রহন করা হবে।
