4. নিচের প্রশ্নগুলির উত্তর দাও [প্রশ্নমান 3]
i). ![]()
উত্তরঃ
![Rendered by QuickLaTeX.com \left ( 987-\overline{43+25} \right )-10\left [ 5+\left \{ (999\div \overline{9\times 3)}+\left ( \overline{8\times 9}\div 6 \right )4 \right \} \right ]\\\\=\left ( 987-68 \right )-10\left [ 5+\left \{ \left ( 999\div 27 \right )+\left ( 72\div 6 \right )4 \right \} \right ]\\\\=919-10\left [ 5+37+12\times 4 \right ]\\\\=919-10\left [ 5+37+48 \right ]\\\\=919-900=19](https://sdtutoronline.com/wp-content/ql-cache/quicklatex.com-e715bc4b847969a02e040d9cc035255e_l3.png)
ii). একটি ইঞ্জিনের সামনের চাকার পরিধি 14 ডেসিমি এবং পিছনের চাকার
পরিধি 35 ডেসিমি। কমপক্ষে কত পথ গেলে চাকা দুটি একেই সঙ্গে পূর্ন্যসংখক
বার ঘোরা সম্পূর্ণ করবে।
উত্তরঃ
ইঞ্জিনের সামনের চাকার পরিধি 14 ডেসিমি এবং পিছনের চাকার পরিধি 35 ডেসিমি,
কমপক্ষে কত পথ গেলে চাকা দুটি একেই সঙ্গে পূর্ন্যসংখ্যক বার ঘুরবে তা হলো 14 ও 35 এর
ল. সা. গু. র সমান হবে ,

![]()
ঘুরবে।
iii). আমার কাছে 20 টাকা আছে। আমি 5 টাকা খরচ করলাম। আমি আমার
টাকার কত অংশ খরচ করলাম ও কত অংশ এখনও আমার কাছে আছে ?
উত্তরঃ
আমার কাছে 20 টাকা আছে , আমি 5 টাকা খরচ করলাম, ![]() আমি আমার টাকার
আমি আমার টাকার ![]() অংশ =
অংশ =![]() অংশ খরচ করলাম
অংশ খরচ করলাম
20 টাকা 5 টাকা খরচ করারর পর আমার কাছে আছে = (20-5)টাকা = 15 টাকা ![]()
iv). আজ টিফিনের সময়ে স্কুলের সুম্পূর্ণ ভরতি জলের ট্যাঙ্কের ![]()
অংশ জল খরচ হয়েছে। ছুটির সময়ে দেখা গেলো আরও ![]() অংশ
অংশ
জল খরচ হয়েছে। ছুটির পর ট্যাঙ্কে কত অংশ জল পড়ে আছে।
উত্তরঃ
ধরি, স্কুলের জলের ট্যাঙ্কের সুম্পূর্ণ আয়তন= 1 অংশ
টিফিনের সময়ে জল খরচ হয়েছে সম্পূর্ণ অংশের ![]() অংশ
অংশ ![]()
এবং ছুটির সময়ে দেখা গেলো আরও খরচ হয়েছে সম্পূর্ণ অংশের
v). ![]() থেকে
থেকে ![]() বিয়োগ করে বিয়োগফলের সঙ্গে কত যোগ করলে 10 পাবো।
বিয়োগ করে বিয়োগফলের সঙ্গে কত যোগ করলে 10 পাবো।
উত্তরঃ
![]() থেকে
থেকে ![]() বিয়োগ করলে বিয়োগফল হবে
বিয়োগ করলে বিয়োগফল হবে ![]()
বিয়োগফলের সঙ্গে কত যোগ করলে 10 হবে তা হলো ![]()
vi). হোস্টেলে 20 জন ছাত্রের 30 দিনের জন্য 150 কিগ্ৰা আটা মজুত রাখা আছে।
কিন্তু 30 কিগ্ৰা আটা নষ্ট হয়েগেছে ও 5 জন ছাত্র বাড়ি চলে গেছে। বাকি আটায়
অবশিষ্ট ছাত্রের কত দিন চলবে।
উত্তরঃ
গণিতের ভাষায় সমস্যাটি হলো :
ছাত্র সংখ্যা(জন) আটার পরিমান (কিগ্ৰা) সময়ের পরিমান (দিন) 20 150 30
(20-5)=15 (150-30)=120 ?
20 জন ছাত্রের 150 কিগ্ৰা আটা দিয়ে চলে 30 দিন
1 জন ছাত্রের 150 কিগ্ৰা আটা দিয়ে চলবে ![]() দিন
দিন
1 জন ছাত্রের 1 কিগ্ৰা আটা দিয়ে চলবে ![]() দিন
দিন
15 জন ছাত্রের 1 কিগ্ৰা আটা দিয়ে চলবে ![]() দিন
দিন
15 জন ছাত্রের 120 কিগ্ৰা আটা দিয়ে চলবে ![]() দিন \
দিন \
= 32 দিন ![]() 15 জন ছাত্রের 120 কিগ্ৰা আটা দিয়ে 32 দিন চলবে।
15 জন ছাত্রের 120 কিগ্ৰা আটা দিয়ে 32 দিন চলবে।
vii). রাম তার টাকার ![]() অংশ দেবনাথকে ও
অংশ দেবনাথকে ও ![]() অংশ
অংশ
সুনিতাকে দেওয়ার পরে তার কাছে 180 টাকা রইল, প্রথমে রামের কাছে কত
টাকা ছিল।
উত্তরঃ
ধরি, প্রথমে রামের কাছে থাকা টাকার পরিমান = 1 অংশ
রামের টাকার ![]() অংশ
অংশ ![]() অংশ
অংশ ![]() অংশ
অংশ ![]() রাম দেবনাথকে দেয়
রাম দেবনাথকে দেয় ![]() অংশ
অংশ
এবং রামের টাকার ![]() অংশ =
অংশ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ ![]() রাম সুনিতা কে দেয় =
রাম সুনিতা কে দেয় = ![]() অংশ
অংশ ![]() দেবনাথ ও সুনিতাকে দেয় মোট =
দেবনাথ ও সুনিতাকে দেয় মোট = ![]() অংশ =
অংশ =![]() অংশ
অংশ ![]() অংশ
অংশ ![]() অংশ
অংশ ![]() দু জন কে দেওয়ার পর রামের কাছে পড়ে থাকে
দু জন কে দেওয়ার পর রামের কাছে পড়ে থাকে ![]() অংশ
অংশ ![]() অংশ প্রশ্নানুসারে,
অংশ প্রশ্নানুসারে, ![]() টাকা
টাকা ![]() 1 অংশ =
1 অংশ = ![]() টাকা = 600 টাকা
টাকা = 600 টাকা ![]() রামের কাছে প্রথমে 600 টাকা ছিল।
রামের কাছে প্রথমে 600 টাকা ছিল।
viii). 5 এর সঙ্গে ![]() যোগ করে যোগফলকে
যোগ করে যোগফলকে ![]() দিয়ে গুন
দিয়ে গুন
করি। এবার ওই গুনফল কে ![]() দিয়ে ভাগ করে ভাগফলটি
দিয়ে ভাগ করে ভাগফলটি ![]() থেকে বিয়োগ করি ও বিয়োগফল কি পেলাম হিসাব করো।
থেকে বিয়োগ করি ও বিয়োগফল কি পেলাম হিসাব করো।
উত্তরঃ
5 এর সঙ্গে ![]() যোগ করলে যোগফল হবে
যোগ করলে যোগফল হবে
=![]()
যোগফল কে ![]() দিয়ে গুন করলে গুনফল হবে
দিয়ে গুন করলে গুনফল হবে
=![]()
গুণফলকে ![]() দিয়ে ভাগ করলে ভাগফলটি হবে
দিয়ে ভাগ করলে ভাগফলটি হবে 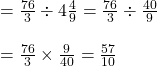 এখন ভাগফলটি কে
এখন ভাগফলটি কে ![]() থেকে বিয়োগ করলে পাবো
থেকে বিয়োগ করলে পাবো 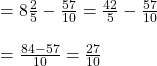
অর্থবা আমরা, এই ভাবে গণিতের ভাষায় লিখে সরল করে মান নির্ণয় করতে পারি, ![]()
ix). সরল করো :![]()
উত্তরঃ
![Rendered by QuickLaTeX.com 1\frac{1}{2}\left [3\frac{1}{2}\div 2\frac{1}{3}\left \{ 1\frac{1}{4}\div \left ( 2+3\frac{2}{3} \right ) \right \} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{7}{3}\left \{ \frac{5}{4}\div \left ( 2+\frac{11}{3} \right ) \right \} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{7}{3}\left \{ \frac{5}{4}\div \frac{17}{3} \right \} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{7}{3}\left \{ \frac{5}{4}\times \frac{3}{17} \right \} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{7}{3}\left \{ \frac{15}{68} \right \} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{7}{3}\times \frac{15}{68} \right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\div \frac{35}{68}\right ]\\\\=\frac{3}{2}\left [ \frac{7}{2}\times \frac{68}{35}\right ]\\\\=\frac{3}{2}\left [ \frac{34}{5}\right ]\\\\= \frac{51}{5}=10\frac{1}{5}](https://sdtutoronline.com/wp-content/ql-cache/quicklatex.com-222223069efbc3d10c0f27be00f84b85_l3.png)
x). গল্প লেখো ও সমাধান করো : ![]()
উত্তরঃ
গল্প : একটি খাতার দাম 13.75 টাকা এবং একটি স্কেলর দাম 12.50 টাকা হলে, রোহিত দোকানে গিয়ে
2টি খাতা ও 3টি স্কেল কিনলো। তাহলে রোহিত দোকানদার কে মোট কত টাকা দেবে।
সমাধান:
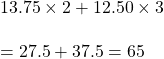
![]() রোহিত দোকানদারকে মোট 65 টাকা দেবে।
রোহিত দোকানদারকে মোট 65 টাকা দেবে।
xi). 15.77 মিটার লম্বা বাঁশের 2.25 অংশ বাদ দিয়ে বাকি অংশকে সমান 4 ভাগে
ভাগ করলে প্রতি ভাগের দৈর্ঘ্য কত হবে।
উত্তরঃ
15.77 মিটার লম্বা বাঁশের 2.25 অংশ বাদ দিলে অবশিষ্ট অংশের দৈর্ঘ্য ![]() মিটার
মিটার ![]() মিটার
মিটার ![]() মিটার কে সমান 4 ভাগে ভাগ করলে প্রতি ভাগের দৈর্ঘ্য হবে
মিটার কে সমান 4 ভাগে ভাগ করলে প্রতি ভাগের দৈর্ঘ্য হবে ![]() মিটার
মিটার
xii). একটি শহরের বর্তমান জনসংখ্যা 26250 জন। যদি বার্ষিক 4% হারে
জনসংখ্যা বাড়ে, তবে পরের বছরের জনসংখ্যা কত হবে হিসাব করো। দুই
বছর পরে জনসংখ্যা কত হবে ?
উত্তরঃ
একটি শহরের জনসংখ্যা 26250 জন, যদি বার্ষিক 4% হারে জনসংখ্যা বাড়ে
তবে পরের বছর জনসংখ্যা হবে = (26250 + 26250 এর 4%)
= (26250+ ![]() ) জন
) জন
= (26250+1050) জন
= 27300 জন ![]() দুই বছর পর জনসংখ্যা হবে = (27300 + 27300 এর 4%) জন
দুই বছর পর জনসংখ্যা হবে = (27300 + 27300 এর 4%) জন
= (27300 +1092 ) জন
= 28392 জন
xiii). গোপালবাবুর মাসিক খরচের 4750 টাকা খাওয়ার জন্যে ব্যয় হয় এবং অন্যান্য খরচ হয় 5900 টাকা। যদি খাওয়ার খরচ 10% বাড়িয়ে অন্যান্য খরচ 16% কমানো হয়, তাহলে মোট মাসিক খরচ বাড়বে না কমবে।
উত্তরঃ
গোপাল বাবুর মাসিক খাওয়ার খরচ হয় = 4750 টাকা এবং
অন্যান্য খরচ হয় = 5900 টাকা ![]() এখন গোপাল বাবুর মোট খরচ হয় = (4750+5900) টাকা = 10,650 টাকা
এখন গোপাল বাবুর মোট খরচ হয় = (4750+5900) টাকা = 10,650 টাকা
যদি খাওয়ার খরচ 10% বাড়ানো হয়, তাহলে এখন গোপাল বাবুর খাওয়ার জন্য খরচ বেড়ে হবে
= (4750 + 4750 এর 10% ) টাকা = (4750 + 475) টাকা = 5225 টাকা
এবং যদি অন্যান্য খরচ 16% কমানো হয়, তাহলে এখন অন্যান্য খরচ কমে হবে
= (5900 – 5900 এর 16%) টাকা = (5900- 944) টাকা = 4956 টাকা ![]() গোপাল বাবুর বর্তমানে মোট খরচ = (5225+4956) টাকা = 10181 টাকা
গোপাল বাবুর বর্তমানে মোট খরচ = (5225+4956) টাকা = 10181 টাকা ![]() বর্তমানে গোপাল বাবুর মাসিক খরচ কমবে = (10650-10181) টাকা = 469 টাকা
বর্তমানে গোপাল বাবুর মাসিক খরচ কমবে = (10650-10181) টাকা = 469 টাকা
xiv). সরল করো : ![]() এর
এর ![]() এর
এর ![]()
উত্তরঃ
![]() এর
এর ![]() এর
এর ![]()
![]() এর
এর ![]() এর
এর ![]()
![]() এর
এর ![]() এর
এর ![]()
![]() এর
এর ![]() এর
এর ![]()
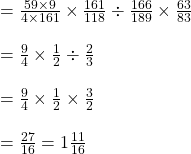
xv). ![]()
উত্তরঃ
![Rendered by QuickLaTeX.com \frac{2}{4}\left [ \overline{2\frac{1}{2}-\frac{3}{4}}\times \frac{4}{7}\times \overline{\frac{1}{4}-\frac{1}{8}} \right ]+\left \{ \frac{3}{4}-\frac{1}{2}+\overline{\frac{1}{4}+\frac{1}{4}} \right \}\times \frac{1}{8}\\\\=\frac{2}{4}\left [ \overline{\frac{10-3}{4}}\times \frac{4}{7} \times \overline{\frac{2-1}{8}}\right ]+\left \{ \frac{3}{4}-\frac{1}{2}+\overline{\frac{1+1}{4}} \right \}\times \frac{1}{8}\\\\=\frac{2}{4}\left [ \frac{7}{4}\times \frac{4}{7} \times \frac{1}{8}\right ]+\left \{ \frac{3}{4}-\frac{1}{2}+\frac{1}{2} \right \}\times \frac{1}{8}\\\\=\frac{2}{4}\left [ \frac{1}{8}\right ]+\left \{ \frac{3}{4}\right \}\times \frac{1}{8}\\\\=\frac{2}{32}+\frac{3}{32}\\\\=\frac{5}{32}](https://sdtutoronline.com/wp-content/ql-cache/quicklatex.com-410ef011181aca9da4ed0d925a2d5abd_l3.png)
xvi). একটি 6 ইঞ্চি লম্বা রেখা প্রথমে রেখাটিকে ![]() ইঞ্চি বাড়ানো হলো এবং
ইঞ্চি বাড়ানো হলো এবং
পরে ![]() ইঞ্চি কমানো হলো, এখন ঐ রেখার
ইঞ্চি কমানো হলো, এখন ঐ রেখার ![]() অংশের দৈর্ঘ্য কত ?
অংশের দৈর্ঘ্য কত ?
উত্তরঃ
6 ইঞ্চি রেখাকে প্রথমে ![]() ইঞ্চি বাড়ানো হলে রেখার দৈর্ঘ্য হবে =
ইঞ্চি বাড়ানো হলে রেখার দৈর্ঘ্য হবে = ![]() ইঞ্চি
ইঞ্চি
পরে রেখাটিকে ![]() ইঞ্চি কমানো হলে , রেখার দর্ঘ্য কমে হবে =
ইঞ্চি কমানো হলে , রেখার দর্ঘ্য কমে হবে = ![]() ইঞ্চি
ইঞ্চি
এখন এই রেখার ![]() অংশের দৈর্ঘ্য =
অংশের দৈর্ঘ্য = ![]() ইঞ্চি
ইঞ্চি ![]() ইঞ্চি
ইঞ্চি
xvii). ![]() হচ্ছে একটি যুগ্ম সংখ্যা। এর আগে ও পরের যুগ্মসংখ্যাগুলি কী কী ?
হচ্ছে একটি যুগ্ম সংখ্যা। এর আগে ও পরের যুগ্মসংখ্যাগুলি কী কী ?
উত্তরঃ
![]() একটি যুগ্ম সংখ্যা হলে তার আগের যুগ্ম সংখ্যা গুলি হবে =
একটি যুগ্ম সংখ্যা হলে তার আগের যুগ্ম সংখ্যা গুলি হবে =![]() এবং
এবং ![]() একটি যুগ্ম সংখ্যা হলে তার পরের যুগ্ম সংখ্যা টি হবে =
একটি যুগ্ম সংখ্যা হলে তার পরের যুগ্ম সংখ্যা টি হবে =![]()
xviii). সংখ্যার সরল রেখার সাহায্যে নিম্নলিখিত সংখ্যাগুলির অবস্থান বোঝাও :
![]()

xix). অর্ঘ 80 টাকায় একটি জিনিস কিনে -15 টাকা লাভে বিক্রি করলো। জিনিসটির বিক্রয়মূল্য কত ? 0 টাকা ক্ষতিতে বিক্রি করলে জিনিসটির বিক্রয়মূল্য কত ?
উত্তরঃ
অর্ঘ 80 টাকায়একটি জিনিস কিনে -15 টাকা লাভে বিক্রি করলে ,
জিনিসটির বিক্রয় মূল্য হবে ![]() টাকা
টাকা ![]() টাকা
টাকা ![]() টাকা
টাকা ![]() টাকা ক্ষতিতে বিক্রয় করলে বিক্রয়মূল্য হবে
টাকা ক্ষতিতে বিক্রয় করলে বিক্রয়মূল্য হবে ![]() টাকা
টাকা ![]() টাকা
টাকা
xx). ![]() ও
ও ![]() এর মান নির্ণয় করো
এর মান নির্ণয় করো
![]()
উত্তরঃ 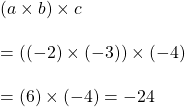
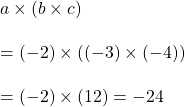
xxi). রসুলপুর গ্রামের জনসংখ্যা গত বছরের তুলনায় 12% বেড়েছে। আগে ওই গ্রামের জনসংখ্যা 775 হলে এখন জনসংখ্যা কত ?
উত্তরঃ
রসুলপুর গ্রামের জনসংখ্যা 12% বেড়েছে , আগে জনসংখ্যা 775 হলে, এখন জনসংখ্যা হবে = (775+ 755 এর 12%) জন
= (775 +93) জন
= 868 জন
xxii). সরল করো :![]()
উত্তরঃ 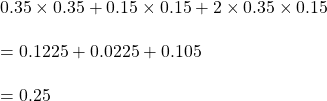
xxiii). একটি সমবাহু ত্রিভুজের পরিসীমা 14.4 সেমি। ওই সমবাহু ত্রিভুজের একটি বাহুর দৈর্ঘ্য কত ?
উত্তরঃ
আমরা জানি যে,
একটি সমবাহু ত্রিভুজের পরিসীমা = ![]() একটি বাহুর দৈর্ঘ্য
একটি বাহুর দৈর্ঘ্য
প্রশ্নানুসারে, ![]() একটি বাহুর দৈর্ঘ্য = 14.4 সেমি
একটি বাহুর দৈর্ঘ্য = 14.4 সেমি ![]() একটি বাহুর দৈর্ঘ্য
একটি বাহুর দৈর্ঘ্য ![]() সেমি
সেমি
![]() সেমি
সেমি
xxiv). সরল করো : ![]()
উত্তরঃ

xxv). ![]() মিটার লম্বা ফিতের
মিটার লম্বা ফিতের ![]() অংশ কেটে নিয়ে তাকে সমান 5 টি ভাগে কাটলে একটি টুকরোর দৈর্ঘ্য কত ?
অংশ কেটে নিয়ে তাকে সমান 5 টি ভাগে কাটলে একটি টুকরোর দৈর্ঘ্য কত ?
উত্তরঃ
![]() মিটার লম্বা ফিতের
মিটার লম্বা ফিতের ![]() অংশ
অংশ ![]() মিটার
মিটার ![]() মিটার
মিটার
![]() মিটার
মিটার
![]() মিটার কে সমান 5 ভাগে কাটলে একটি টুকরোর দৈর্ঘ্য
মিটার কে সমান 5 ভাগে কাটলে একটি টুকরোর দৈর্ঘ্য ![]() মিটার
মিটার
![]() মিটার
মিটার
![]() মিটার
মিটার ![]() মিটার
মিটার
xxvi). শহরের একটি অনুষ্ঠানে প্রথম বছর 1400 জন দর্শক এসেছিলেন। পরের বছর দর্শক সংখ্যা প্রথম বছরের থেকে ![]() অংশ বেড়ে গেলো। পরের বছরে মোট কতজন দর্শক এসেছিলো?
অংশ বেড়ে গেলো। পরের বছরে মোট কতজন দর্শক এসেছিলো?
উত্তরঃ
শহরের একটি অনুষ্ঠানে প্রথম বছরে 1400 জন দর্শক এসেছিলেন ,
পরের বছরে দর্শক সংখ্যা প্রথম বছরের ![]() অংশ বেড়েছিল
অংশ বেড়েছিল ![]() পরের বছরে দর্শক বেবেড়েছিলো = 1400 এর
পরের বছরে দর্শক বেবেড়েছিলো = 1400 এর ![]() জন
জন
![]() জন
জন ![]() জন
জন ![]() পরের বছরের মোট
পরের বছরের মোট ![]() জন
জন ![]() জন দর্শক এসেছিলো।
জন দর্শক এসেছিলো।
xxvii). পার্থ ও তীর্থ দুজন পুকুরের পাড়ে বসে মাছ ধরছে। তীর্থ যতগুলি মাছ ধরলো পার্থ তার থেকে 5 টি বেশি মাছ ধরলো। পার্থ কতগুলি মাছ ধরলো তা তীর্থের ধরা মাছের সংখ্যা দিয়ে প্রকাশ করো।
উত্তরঃ
ধরি, তীর্থ ![]() টি মাছ ধরলো,
টি মাছ ধরলো,
পার্থ, তীর্থের থেকে 5 টি মাছ বেশি ধরলো![]() পার্থের ধরা মাছের সংখ্যা
পার্থের ধরা মাছের সংখ্যা ![]() টি
টি
xxviii). 15 টি ভ্যান 40 মিনিটে 75 কুইন্টাল সব্জি টানতে পারে। 20 টি ভ্যান 1000 কুইন্টাল সব্জি টানতে কত সময় নেবে ?
উত্তরঃ
গণিতের ভাষায় সমস্যাটি হলো :
ভ্যানের সংখ্যা (টি ) সব্জির পরিমান (কু 🙂 সময়ের পরিমান (মিনিট)
15 75 40
20 1000 ?
15টি ভ্যান 75 কুইন্টাল সব্জি টানতে পারে 40 মিনিটে
1 টি ভ্যান 75 কুইন্টাল সবজি টানতে পারে ![]() মিনিটে
মিনিটে
1 টি ভ্যান 1 কুইন্টাল সব্জি টানতে পারে ![]() মিনিটে
মিনিটে
20 টি ভ্যান 1 কুইন্টাল সব্জি টানতে পারে ![]() মিনিটে
মিনিটে
20 টি ভ্যান 1000 কুইন্টাল সব্জি টানতে পারে ![]() মিনিটে
মিনিটে
= 400 মিনিটে ![]() 20 টি ভ্যান 1000 কুইন্টাল সবজি টানতে পারে 400 মিনিটে।
20 টি ভ্যান 1000 কুইন্টাল সবজি টানতে পারে 400 মিনিটে।
xxix). উদ্ধক্রমে সাজাও : ![]()
উত্তরঃ
উদ্ধক্রমে সাজানোর জন্যে আমরা প্রথমে এই দশমিক সংখ্যাগুলিকে দশমিকের পরের অংশটা সমান
ঘরে পরিণত করবো,
এর পর আমরা এই সংখ্যাগুলিকে ভগ্নাংশে পরিণত করে পাই ,
ভগ্নাংশগুলির হর সমান, যার লব বড়ো সেই সংখ্যাটি বড়ো অন্যটির থেকে,![]() মানের উদ্ধক্রমে সাজিয়ে পাই,
মানের উদ্ধক্রমে সাজিয়ে পাই, ![]()
xxx). আমার কাছে 20 টাকা আছে। আমি 5 টাকা খরচ করলাম। আমি আমার টাকার কত অংশ খরচ করলাম এবং কত অংশ আমার কাছে আছে ?
উত্তরঃ
আমার কাছে আছে মোট টাকা = 20 টাকা
আমি খরচ করলাম = 5 টাকা ![]() আমি আমার টাকার
আমি আমার টাকার ![]() অংশ
অংশ ![]() অংশ খরচ করলাম,
অংশ খরচ করলাম,
5 টাকা খরচ করার পর আমার কাছে আছে এখন = (20-5) টাকা =15![]() আমার কাছে এখন আমার টাকার
আমার কাছে এখন আমার টাকার ![]() অংশ
অংশ ![]() অংশ আছে।
অংশ আছে।
CLASS-VI-দাগ নাম্বার -1 &2-Annual Examination—2021/MODEL QUESTION/Mathematics:
http://sdtutoronline.com/question12-annualexamination2021modelquestionvimathematics/
CLASS-VI-দাগ নাম্বার -3 & 4-Annual Examination—2021/MODEL QUESTION/Mathematics:
http://sdtutoronline.com/class-vi-3-4-annual-mathematics/
