Annual Examination—2021
MODEL QUESTION SOLVED-দাগ নাম্বার -4 & 5
Class — V
Subject : Mathematics
………………………………………………………………………………………………..
সমাধানঃ
সত্য

সমাধানঃ সত্য
আয়তকার মাঠের পরিসীমা = 360 মিটার
আয়তকার মাঠের দৈর্ঘ্য =100 মিটার
আয়তক্ষেত্রের পরিসীমা = 2 (দৈর্ঘ্য +প্রস্থ )
সমাধানঃ মিথ্যা
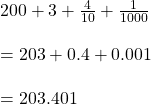

সমাধানঃ সত্য
বাঁশের মোট দৈর্ঘ্য = 14.09 মিটার
কাদায় ও জলে আছে মোট = (4.2+3.01) মিটার = 7.21 মিটার
কাদার ও জলের উপরে আছে = (14.09-7.21) মিটার = 6.88 মিটার

সমাধানঃ সত্য
ইয়াসিন 200 টাকায় কিনে 1000 গ্রাম চা
ইয়াসিন 1 টাকায় কিনবে 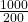 গ্রাম চা
গ্রাম চা
ইয়াসিন 50 টাকায় কিনবে 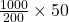 গ্রাম চা = 250 গ্রাম চা
গ্রাম চা = 250 গ্রাম চা

সমাধানঃ
মিথ্যা
কাজের পরিমাণ নির্দিষ্ট থাকলে নাঙলের সংখ্যার সঙ্গে দিন সংখ্যা ব্যস্ত সম্পর্ক
![]()
সমাধানঃ সত্য


![]()
সমাধানঃ সত্য
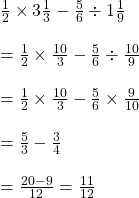
![]()
সমাধানঃ মিথ্যা
1 আর = 100 বর্গ মিটার
5 আর = 500 বর্গমিটার

সমাধানঃ মিথ্যা

সমাধানঃ সত্য
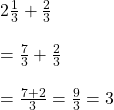
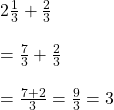
![]()
সমাধানঃ মিথ্যা
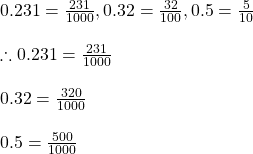
সবথেকে ক্ষুদ্রতম সংখ্যাটি হল = 0.231

সমাধানঃ সত্য

সমাধানঃ সত্য
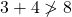

সমাধানঃ মিথ্যা
তিনটি বাহু দ্বারা ত্রিভুজ অঙ্কন সম্ভভ হবে যদি, যে কোন দুটি বাহুর যোগফল তৃতীয় বাহুর থেকে যদি বড়ো হয়

সমাধানঃ
ধরি, চৌবাচ্চার মোট অংশ = 1 অংশ
চৌবাচ্চায় আগে থেকে জল ছিল 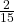 অংশ
অংশ
আমি চৌবাচ্চায় জল ঢাললাম = 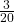 অংশ
অংশ
দাদা জল ঢালল = 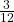 অংশ
অংশ
এখন চৌবাচ্চায় মোট জলের পরিমাণ = 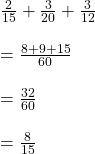
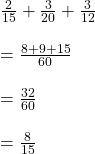
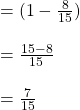

সমাধানঃ
আয়তকার মাঠের পরিসীমা = 256 মিটার
আয়তকার মাঠের দৈর্ঘ্য =74 মিটার
আয়তক্ষেত্রের পরিসীমা = 2 (দৈর্ঘ্য +প্রস্থ )
= 3996 বর্গমিটার

সমাধানঃ
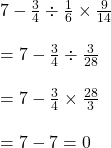

সমাধানঃ

সমাধানঃ
ভগ্নাংশটি  অপেক্ষা যত বড়ো,
অপেক্ষা যত বড়ো,  অপেক্ষা তত ছোট ,
অপেক্ষা তত ছোট ,
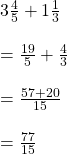

সমাধানঃ
ধরি, দুটি খণ্ডকে একটি কে প্রথম খণ্ড আর অন্যটি কে দ্বিতীয় খণ্ড
প্রশ্নানুসারে,
প্রথম খণ্ড + দ্বিতীয় খণ্ড = 168 গজ

সমাধানঃ
ধরি, মোট সম্পত্তির পরিমাণ = 1 অংশ
সম্পত্তির 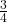 অংশ = 1 এর
অংশ = 1 এর 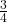 অংশ =
অংশ = 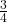 অংশ
অংশ
সম্পত্তির 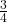 অংশের মূল্য 3300 টাকা
অংশের মূল্য 3300 টাকা
সম্পত্তির 1 অংশ = সমগ্র অংশের মূল্য = 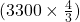 টাকা =
টাকা = 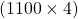 টাকা = 4400 টাকা
টাকা = 4400 টাকা
সম্পত্তির 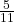 অংশের মূল্য =
অংশের মূল্য = 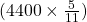 টাকা = 2000 টাকা
টাকা = 2000 টাকা

সমাধানঃ
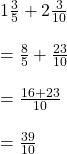


সমাধানঃ
বস্তায় মোট আলুর পরিমাণ 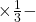 বস্তায় মোট আলুর পরিমাণ
বস্তায় মোট আলুর পরিমাণ 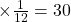 কেজি
কেজি

সমাধানঃ
100 বর্গ ডেসিমিটার = 1 বর্গ মিটার
আয়তক্ষেত্রের কালি / ক্ষেত্রফল = 18 বর্গমিটার 60 বর্গ ডেসিমিটার = 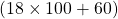 বর্গ ডেসিমিটার= 1860 বর্গ ডেসিমিটার
বর্গ ডেসিমিটার= 1860 বর্গ ডেসিমিটার
আয়তক্ষেত্রের কালি / ক্ষেত্রফল = দৈর্ঘ্য 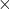 প্রস্থ
প্রস্থ
আয়তক্ষেত্রের প্রস্থ = 3 মিটার = 30 ডেসিমিটার
আয়তক্ষেত্রের দৈর্ঘ্য = 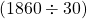 ডেসিমিটার= 62 ডেসিমিটার= 6.2 মিটার
ডেসিমিটার= 62 ডেসিমিটার= 6.2 মিটার

সমাধানঃ
1 গজ = 3 ফুট
6 গজ = 18 ফুট
18 ফুট বর্গ উঠানের ক্ষেত্রফল = 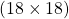 বর্গফুট = 324 বর্গফুট
বর্গফুট = 324 বর্গফুট
3 ফুট বর্গ টালির ক্ষেত্রফল = 9 বর্গফুট
টালি দিয়েউথন্তি ঢাকতে মোট টালি লাগবে = 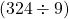 টি = 36 টি
টি = 36 টি

সমাধানঃ
1 আর = 100 বর্গ মিটার
1.44 আর = 144 বর্গমিটার
বর্গ ক্ষেত্রের ক্ষেত্রফল = 144 বর্গমিটার
বর্গ ক্ষেত্রের একটি বাহুর দৈর্ঘ্য = 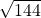 মিটার = 12 মিটার
মিটার = 12 মিটার
বর্গক্ষেত্রের পরিসীমা = 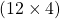 মিটার = 48 মিটার
মিটার = 48 মিটার

সমাধানঃ
আয়তক্ষেত্রের প্রস্থ = 16 মিটার
আয়তক্ষেত্রের দৈর্ঘ্য = 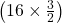 মিটার = 24 মিটার
মিটার = 24 মিটার
আয়তক্ষেত্রের পরিসীমা = 2 (দৈর্ঘ্য +প্রস্থ )

সমাধানঃ
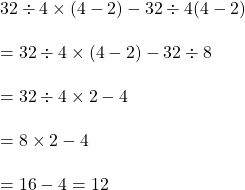

সমাধানঃ
আয়তকার পার্কের দৈর্ঘ্য = 25 মিটার
আয়তকার পার্কের প্রস্থ = 15 মিটার
আয়তকার পার্কের পরিসীমা = 2 (দৈর্ঘ্য +প্রস্থ ) একক
= 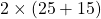 মিটার = 80 মিটার
মিটার = 80 মিটার
প্রত্যেক ধারের দৈর্ঘ্য 2 মিটার করে বাড়ানো হলে পার্কের দৈর্ঘ্য হবে = 27 মিটার
আয়তকার পার্কের প্রস্থ হবে = 17 মিটার
আয়তকার পার্কের পরিসীমা হবে = 2 (দৈর্ঘ্য +প্রস্থ ) একক
= 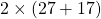 মিটার = 88 মিটার
মিটার = 88 মিটার

সমাধানঃ
গণিতের ভাষায় সমস্যাটি হলঃ
লোক সংখ্যা দিন সংখ্যা
21 40
(21-7) = 14 ?
21 জন লোক 40 দিনে পুকুরটি খনন করতেপারে
1 জন লোকের পুকুরটি খনন করতে সময় লাগবে = 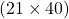 দিন = 840 দিন
দিন = 840 দিন
14 জন লোকের পুকুরটি খনন করতে সময় লাগবে =  দিন = 60 দিন
দিন = 60 দিন

সমাধানঃ
গণিতের ভাষায় সমস্যাটি হলঃ
মুরগির সংখ্যা দিন সংখ্যা
4000 250
(4000+1000) = 5000 ?
মজুত খাবার 4000 টি মুরগির চলবে 250 দিন
মজুত খাবার 1 টি মুরগির চলবে = 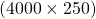 দিন = 10000000 দিন
দিন = 10000000 দিন
মজুত খাবার 5000 টি মুরগির চলবে = 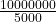 দিন = 200 দিন
দিন = 200 দিন

সমাধানঃ
গণিতের ভাষায় সমস্যাটি হলঃ
দূরত্ব (মিটার ) চাকা ঘুরার পরিমাণ (বার)
170 51
1700 ?
চাকা টি 170 মিটার যেতে 51 বার ঘুরে
চাকা টি 1 মিটার যেতে ঘুরবে = 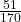 বার
বার
চাকা টি 1700 মিটার যেতে ঘুরবে = 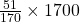 বার = 510 বার
বার = 510 বার

সমাধানঃ
চৌবাচ্চায় প্রথমে জল ছিল =  লিটার
লিটার
সেখান থেকে  লিটার জল খরচ হয়েছে
লিটার জল খরচ হয়েছে
খরচ হওয়ার পর এখন চৌবাচ্চায় জল আছে = 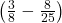 লিটার =
লিটার = 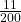 লিটার
লিটার
আমি বালতি করে চৌবাচ্চায় আরও 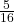 লিটার জল ঢাললাম
লিটার জল ঢাললাম
= 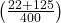 লিটার =
লিটার = 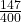 লিটার
লিটার

সমাধানঃ
মডেল প্রশ্ন দাগ নাম্বার -১ এর লিঙ্ক :
https://www.sdtutoronline.com/2021/11/class-v-math-sample-questions-solved.html
এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।



Skidson