Annual Examination—2021
MODEL QUESTION SOLVED-দাগ নাম্বার -: 3
Class — VIII
Subject : Mathematics
এই পোস্ট টি তে class-VIII / Class-8 এর বীজগণিত , পাটিগণিত এর কিছু গুরুত্বপূর্ণ সমস্যা /ছোট প্রশ্ন (Short questions/ Very short question (VSQ)) সমাধান করা হয়েছে ।
সমস্যা গুলি মূলত WB-Chapter-মিশ্রণ (Mixture) – প্রশ্নমালা/ কষে দেখি -12, লেখচিত্র (Graph) – কষে দেখি/ প্রশ্নমালা -18, বীজগাণিতিক সংখ্যামালার উৎপাদক বিশ্লেষণ ( Factorization of algebraic expression) কষে দেখি/ প্রশ্নমালা -13, বীজগাণিতিক সংখ্যামালার লসাগু ও গসাগু (LCM, HCF of algebraic expression)- কষে দেখি/ প্রশ্নমালা -14, বীজগাণিতিক সংখ্যামালার সরলীকরণ (Simplification of algebraic expression) – কষে দেখি/ প্রশ্নমালা -15, সমীকরণ গঠন ও সমাধান (Equation formation and solution ) কষে দেখি/ প্রশ্নমালা -19, ত্রৈরাশিক (Rule of three) কষে দেখি/ প্রশ্নমালা -10, শতকরা (Percentage) কষে দেখি/ প্রশ্নমালা -11 এর অন্তর্গত ।
3. নিম্ন লিখিত প্রশ্ন গুলির উত্তর দাও [প্রশ্নমান 2 ]

36 লিটার ডেটল-জল তৈরি করলাম যাতে জল ও ডেটলের পরিমাণের অনুপাত 5:1
![]() 36 লিটার ডেটল-জলে জলের আনুপাতিক ভাগহার =
36 লিটার ডেটল-জলে জলের আনুপাতিক ভাগহার = ![]()
এবং 36 লিটার ডেটল-জলে ডেটলের আনুপাতিক ভাগহার = ![]()
![]() 36 লিটার ডেটল-জলে জলের পরিমাণ =
36 লিটার ডেটল-জলে জলের পরিমাণ = ![]() লিটার
লিটার
এবং 36 লিটার ডেটল-জলে ডেটলের পরিমাণ = ![]()
ধরি ওই ডেটল জলে আরও ![]() লিটার ডেটল মেশালে জল ও ডেটলের পরিমাণের অনুপাত 3:1 হবে ।
লিটার ডেটল মেশালে জল ও ডেটলের পরিমাণের অনুপাত 3:1 হবে ।
![]() ডেটল জলে আরও
ডেটল জলে আরও ![]() লিটার ডেটল মেশালে ডেটলের পরিমাণ হবে
লিটার ডেটল মেশালে ডেটলের পরিমাণ হবে ![]() লিটার এবং জলের পরিমাণ হবে 30 লিটার
লিটার এবং জলের পরিমাণ হবে 30 লিটার
প্রশ্নানুসারে,

![]()

সমাধানঃ
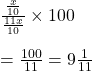

8 টি গরুর 4 কাহন খড় খেতে সময় লাগে 15 দিন, এই রকম 10 টি গরুর 24 কাহন খড় খেতে কত দিন সময় লাগবে ।
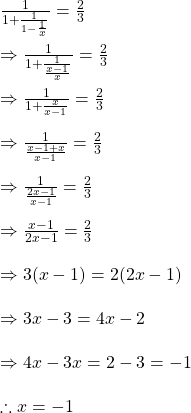




সমাধানঃ
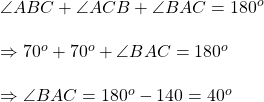


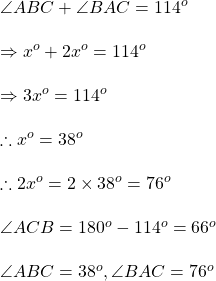

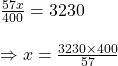

এক ধরনের পিতলে তামা ও দস্তার পরিমাণের অনুপাত 5:2
![]() 28 কিগ্রা পিতলে তামার আনুপাতিক ভাগহার =
28 কিগ্রা পিতলে তামার আনুপাতিক ভাগহার = ![]()
এবং 28 কিগ্রা পিতলে দস্তার আনুপাতিক ভাগহার = ![]()
![]() 28 কিগ্রা পিতলে তামার পরিমাণ =
28 কিগ্রা পিতলে তামার পরিমাণ = ![]() কিগ্রা
কিগ্রা
এবং 28 কিগ্রা পিতলে দস্তার পরিমাণ = ![]() কিগ্রা
কিগ্রা
28 কিগ্রা পিতলে 4 কিগ্রা তামা মেশালে তামার পরিমাণ হবে = (20+4) কিগ্রা = 24 কিগ্রা
![]() 28 কিগ্রা পিতলের 4 কিগ্রা তামা মেশালে তামা ও দস্তার পরিমাণের অনুপাত হবে = 24: 8=3:1
28 কিগ্রা পিতলের 4 কিগ্রা তামা মেশালে তামা ও দস্তার পরিমাণের অনুপাত হবে = 24: 8=3:1

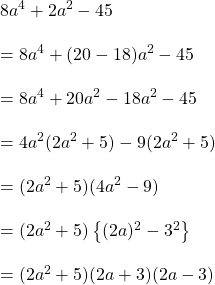

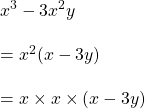
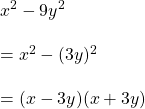

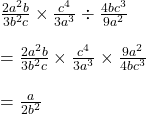

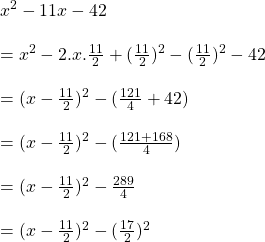

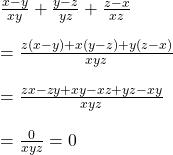

সমাধানঃ
ধরি, পাত্রের আয়তন ![]() ঘন একক
ঘন একক
একপাত্র শরবতে 5:2 অনুপাতে সিরাপ ও জল মেশানো আছে ।
![]() ঘন একক শরবতে সিরাপ আছে =
ঘন একক শরবতে সিরাপ আছে = ![]() ঘন একক, এবং জল আছে =
ঘন একক, এবং জল আছে = ![]() ঘন একক
ঘন একক
ধরি, এই শরবতের ![]() অংশ তুলে নিয়ে তাঁর পরিবর্তে সমপরিমাণ জল ঢাললে সিরাপ ও জলের পরিমাণ সমান সমান হবে ।
অংশ তুলে নিয়ে তাঁর পরিবর্তে সমপরিমাণ জল ঢাললে সিরাপ ও জলের পরিমাণ সমান সমান হবে ।
![]() অংশে শরবতে সিরাপ থাকবে =
অংশে শরবতে সিরাপ থাকবে = ![]() অংশ
অংশ
![]() অংশে শরবতে জল থাকবে =
অংশে শরবতে জল থাকবে = ![]() অংশ
অংশ
এখন শরবতে ![]() অংশ জল ঢাললে, জলের পরিমাণ হবে =
অংশ জল ঢাললে, জলের পরিমাণ হবে = ![]() ঘন একক
ঘন একক
এখন শরবতে সিরাপের পরিমাণ হবে = ![]() ঘন একক,
ঘন একক,
প্রশ্নানুসারে,

![]() এই শরবতের
এই শরবতের ![]() অংশ তুলে নিয়ে তাঁর পরিবর্তে সমপরিমাণ জল ঢাললে সিরাপ ও জলের পরিমাণ সমান সমান হবে ।
অংশ তুলে নিয়ে তাঁর পরিবর্তে সমপরিমাণ জল ঢাললে সিরাপ ও জলের পরিমাণ সমান সমান হবে ।

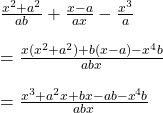

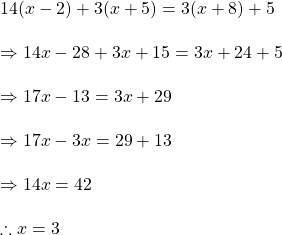
1. Class -VIII/ Model activity task / বহু বিকল্পভিত্তিক প্রশ্নঃ পরিচিতি ও অনুশীলনী গণিত/ অষ্টম শ্রেণী : LINK: https://www.sdtutoronline.com/2021/10/WB-Class-VIII-Model-activity-task-Math-8.html
2. Class-VIII-দাগ নাম্বার – 1 & 2-Annual Examination—2021/MODEL QUESTION/Mathematics : LINK:
এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।