……………………………………………….
Class-V/5
K. C. NAG-প্রশ্নমালা -30
পাটি গণিত
……………………………………………………………………………………………….
1. 15 মিটার, 9 মিটারের কত গুন ? কোন সংখ্যার ![]()
সমাধানঃ
15 মিটার, 9 মিটারের কত গুন বের করতে গেলে আমরা 15 মিটার কে 9 মিটার দিয়ে ভাগ করতে হবে
![]() 15 মিটার, 9 মিটারের
15 মিটার, 9 মিটারের ![]() গুন =
গুন = ![]()
কোন সংখ্যার ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
নির্ণেয় সংখ্যা = ![]()
2. 12 দিন কে 8 দিনের ভগ্নাংশে পরিণত করো ।
সমাধানঃ
12 দিনকে 8 দিনের ভগ্নাংশে পরিণত করলে হবে = ![]()
3. ![]() এর সহিত কতো যোগ করলে
এর সহিত কতো যোগ করলে ![]() হবে ।
হবে ।
সমাধানঃ
![]() + নির্ণেয় সংখ্যা =
+ নির্ণেয় সংখ্যা = ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]()
4. ![]()
![]() অবশিষ্ট থাকবে ?
অবশিষ্ট থাকবে ?
সমাধানঃ
![]() – নির্ণেয় সংখ্যা =
– নির্ণেয় সংখ্যা = ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]() –
– ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]()
5. ![]() এর
এর ![]() হইতে কত বিয়োগ করিলে
হইতে কত বিয়োগ করিলে ![]() এর
এর ![]() বাকী থাকে ?
বাকী থাকে ?
সমাধানঃ
![]() এর
এর ![]() হইতে কত বিয়োগ করিলে
হইতে কত বিয়োগ করিলে ![]() এর
এর ![]() বাকী থাকে তা হোল
বাকী থাকে তা হোল
= ![]() এর
এর ![]() –
–![]() এর
এর ![]()
= ![]()
= ![]() =
= ![]() =
= ![]()
![]()
![]() এর
এর ![]() হইতে
হইতে ![]() বিয়োগ করিলে
বিয়োগ করিলে ![]() এর
এর ![]() বাকী থাকে .
বাকী থাকে .
6. কোন সংখ্যার সহিত ![]() এর
এর ![]() যোগ করিলে
যোগ করিলে ![]() হবে ?
হবে ?
সমাধানঃ
![]() নির্ণেয় সংখ্যা +
নির্ণেয় সংখ্যা + ![]() এর
এর ![]() =
= ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]() –
– ![]() এর
এর ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]() –
– ![]()
![]() নির্ণেয় সংখ্যা =
নির্ণেয় সংখ্যা = ![]()
![]()
![]() এর সহিত
এর সহিত ![]() এর
এর ![]() যোগ করিলে
যোগ করিলে ![]() হবে ।
হবে ।
7. ![]() এর সহিত কোন ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে ।
এর সহিত কোন ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে ।
সমাধানঃ
![]() এর ঠিক পরের/ কাছের পূর্ণ সংখ্যা হোল 3,
এর ঠিক পরের/ কাছের পূর্ণ সংখ্যা হোল 3,
![]()
![]() এর সহিত যে ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে তা হোল
এর সহিত যে ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে তা হোল
= ![]()
![]()
![]() এর সহিত
এর সহিত ![]() ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে।
ক্ষুদ্রতম সংখ্যা যোগ করিলে একটি পূর্ণ সংখ্যা হবে।
8. দুইটি সংখ্যার যোগফল ![]() , উহাদের মধ্যে একটি
, উহাদের মধ্যে একটি ![]() হইলে অন্যটি কত ?
হইলে অন্যটি কত ?
সমাধানঃ
দুইটি সংখ্যার যোগফল =![]()
উহাদের মধ্যে একটি =![]()
![]() অন্যটি সংখ্যাটি =
অন্যটি সংখ্যাটি = 
![]() দুইটি সংখ্যার যোগফল
দুইটি সংখ্যার যোগফল ![]() , উহাদের মধ্যে একটি
, উহাদের মধ্যে একটি ![]() হইলে অন্যটি
হইলে অন্যটি ![]()
9. দুইটি সংখ্যার যোগফল ![]() এবং অন্তর
এবং অন্তর ![]() , সংখ্যা দুইটি নির্ণয় করো ।
, সংখ্যা দুইটি নির্ণয় করো ।
সমাধানঃ
দুইটি সংখ্যার যোগফল ![]() + দুটি সংখ্যার অন্তর
+ দুটি সংখ্যার অন্তর ![]() =
= ![]() বড়ো সংখ্যা
বড়ো সংখ্যা
![]()
![]() বড়ো সংখ্যা =
বড়ো সংখ্যা = ![]() +
+ ![]()
![]()
![]() বড়ো সংখ্যা =
বড়ো সংখ্যা = ![]() +
+ ![]()
![]() বড়ো সংখ্যা =
বড়ো সংখ্যা =![]()
![]() ছোটো সংখ্যা =
ছোটো সংখ্যা = ![]()
10. দুইটি সংখ্যার একটি অন্যটির অপেক্ষা ![]() বেশি । যদি উহাদের মধ্যে ক্ষুদ্রতর সংখ্যাটি
বেশি । যদি উহাদের মধ্যে ক্ষুদ্রতর সংখ্যাটি ![]() অপেক্ষা
অপেক্ষা ![]() কম হয়, তবে সংখ্যা দুইটি কি কি ।
কম হয়, তবে সংখ্যা দুইটি কি কি ।
সমাধানঃ
দুইটি সংখ্যার মধ্যে ক্ষুদ্রতর সংখ্যাটি ![]() অপেক্ষা
অপেক্ষা ![]() কম অর্থাৎ ক্ষুদ্রতর সংখ্যাটি =
কম অর্থাৎ ক্ষুদ্রতর সংখ্যাটি =  যেহেতু, দুইটি সংখ্যার, একটি অন্যটির অপেক্ষা
যেহেতু, দুইটি সংখ্যার, একটি অন্যটির অপেক্ষা ![]() বেশি এবং ক্ষুদ্রতর সংখ্যাটি = .
বেশি এবং ক্ষুদ্রতর সংখ্যাটি = .![]()
![]() বৃহত্তর সংখ্যাটি =
বৃহত্তর সংখ্যাটি = 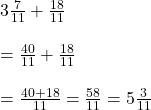
![]() সংখ্যা দুইটি হোলঃ বৃহত্তর সংখ্যাটি =
সংখ্যা দুইটি হোলঃ বৃহত্তর সংখ্যাটি = ![]()
![]() ক্ষুদ্রতর সংখ্যাটি = .
ক্ষুদ্রতর সংখ্যাটি = .![]()
11. ![]() ও
ও ![]() এর সমষ্টির মধ্যে
এর সমষ্টির মধ্যে ![]() ও
ও ![]() এর অন্তর টি কত বার আছে ?
এর অন্তর টি কত বার আছে ?
সমাধানঃ
![]() ও
ও ![]() এর সমষ্টি
এর সমষ্টি
= 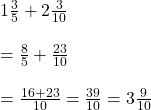
এবং
![]() ও
ও ![]() এর অন্তর =
এর অন্তর = 
![]() ও
ও ![]() এর সমষ্টির মধ্যে
এর সমষ্টির মধ্যে ![]() ও
ও ![]() এর অন্তর টি আছে
এর অন্তর টি আছে
= 
12. গুণ্য ![]() এবং গুণফল
এবং গুণফল ![]() হইলে গুনক টি কত ?
হইলে গুনক টি কত ?
সমাধানঃ
আমরা জানি যে, গুণ্য ![]() গুনক = গুণফল
গুনক = গুণফল
![]()
![]() গুনক =
গুনক =![]()
![]() গুনক =
গুনক = ![]()
13. ভাজক ![]() এবং ভাগফল ভাজকের
এবং ভাগফল ভাজকের ![]() হইলে ভাজ্য কত ?
হইলে ভাজ্য কত ?
সমাধানঃ
আমরা জানি যে, ভাজ্য = ভাজক ![]() ভাগফল + ভাগশেষ
ভাগফল + ভাগশেষ
ভাজক = ![]()
ভাগফল = ভাজকের ![]() =
= ![]()
ধরি, ভাগশেষ = ![]()
ভাজ্য= ভাজক ![]() ভাগফল
ভাগফল
![]() ভাজ্য=
ভাজ্য= ![]()
![]()
![]() ভাজ্য =
ভাজ্য = ![]()
![]() ভাজক
ভাজক ![]() এবং ভাগফল ভাজকের
এবং ভাগফল ভাজকের ![]() হইলে ভাজ্য =
হইলে ভাজ্য = ![]()
14. কোন দুইটি সংখ্যার একটিতে ![]() এর
এর ![]() দিয়া গুন করলে গুণফল 7 হইবে এবং অন্যটিকে ভাগ করলে ভাগফল
দিয়া গুন করলে গুণফল 7 হইবে এবং অন্যটিকে ভাগ করলে ভাগফল ![]() হইবে ?
হইবে ?
সমাধানঃ
ধরি, একটি সংখ্যা = ক এবং অন্য সংখ্যাটি = খ
প্রশ্নানুসারে, ক ![]() এর
এর ![]() এবং খ
এবং খ ![]() এর
এর ![]()
![]() ক
ক ![]() এর
এর ![]()
![]() ক
ক ![]()
![]() ক
ক ![]()
![]() ক
ক ![]() এবং খ
এবং খ ![]() এর
এর ![]()
![]() খ
খ ![]()
![]() খ
খ ![]()
![]() খ
খ ![]()
![]() একটি সংখ্যা
একটি সংখ্যা ![]() এবং অন্য সংখ্যাটি =
এবং অন্য সংখ্যাটি = ![]()
15. ![]() কে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুন করলে গুণফল একটি অখণ্ড সংখ্যা হবে ।
কে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুন করলে গুণফল একটি অখণ্ড সংখ্যা হবে ।
সমাধানঃ
যেহেতু ![]() সংখ্যাটি 1 এর থেকে ছোটো
সংখ্যাটি 1 এর থেকে ছোটো
![]() সব থেকে ক্ষুদ্রতম সংখ্যা দিয়ে গুন করলে যে অখণ্ড সংখ্যা পাবো তা হবে 1
সব থেকে ক্ষুদ্রতম সংখ্যা দিয়ে গুন করলে যে অখণ্ড সংখ্যা পাবো তা হবে 1
ধরি, ![]() কে -ক দিয়ে গুন করলে গুণফল = 1 হবে
কে -ক দিয়ে গুন করলে গুণফল = 1 হবে ![]() ক
ক ![]()
![]() ক
ক ![]()
![]() ক
ক ![]()
![]() নির্ণেয় ক্ষুদ্রতম সংখ্যা যা দিয়ে
নির্ণেয় ক্ষুদ্রতম সংখ্যা যা দিয়ে ![]() কে গুন করলে গুণফল একটি অখণ্ড সংখ্যা হবে তা হোল
কে গুন করলে গুণফল একটি অখণ্ড সংখ্যা হবে তা হোল ![]()
16. ![]() কে কোন বৃহত্তম সংখ্যা দ্বারা ভাগ করলে ভাগফল একটি পূর্ণসংখ্যা হবে ?
কে কোন বৃহত্তম সংখ্যা দ্বারা ভাগ করলে ভাগফল একটি পূর্ণসংখ্যা হবে ?
সমাধানঃ
![]() এই সংখ্যাটি পূর্ণ সংখ্যা হবে যদি 15 বা 15 এর গুণিতক দিয়ে গুন করা হয় অর্থাৎ 15, 30, 45, 60,……, দিয়ে গুন করা হয়
এই সংখ্যাটি পূর্ণ সংখ্যা হবে যদি 15 বা 15 এর গুণিতক দিয়ে গুন করা হয় অর্থাৎ 15, 30, 45, 60,……, দিয়ে গুন করা হয়
![]() এই সংখ্যাটি পূর্ণ সংখ্যা হবে যদি
এই সংখ্যাটি পূর্ণ সংখ্যা হবে যদি ![]() দিয়ে ভাগ করা হয়,
দিয়ে ভাগ করা হয়,
![]() এদের মধ্যে বৃহত্তম সংখ্যাটি হোল
এদের মধ্যে বৃহত্তম সংখ্যাটি হোল ![]() কিন্তু আমরা জানি যে কোনও সংখ্যাকে ওই সংখ্যা দিয়ে ভাগ করলে পূর্ণ সংখ্যা পাওয়া যাবে ।
কিন্তু আমরা জানি যে কোনও সংখ্যাকে ওই সংখ্যা দিয়ে ভাগ করলে পূর্ণ সংখ্যা পাওয়া যাবে ।
![]()
![]() এই সংখ্যাটি কে
এই সংখ্যাটি কে ![]() দিয়ে ভাগ করলে পূর্ণ সংখ্যা হবে এবং পূর্ণ সংখ্যা টি হোল =1
দিয়ে ভাগ করলে পূর্ণ সংখ্যা হবে এবং পূর্ণ সংখ্যা টি হোল =1
এবার দেখছি যে, ![]() এবং
এবং ![]() এর মধ্যে বৃহত্তম সংখ্যা হোল =
এর মধ্যে বৃহত্তম সংখ্যা হোল = ![]()
![]()
![]() এই সংখ্যাটি কে
এই সংখ্যাটি কে![]() দিয়ে ভাগ করলে পূর্ণ সংখ্যা হবে ।
দিয়ে ভাগ করলে পূর্ণ সংখ্যা হবে ।
17. ![]() এর সহিত উহার কত অংশ যোগ করলে,
এর সহিত উহার কত অংশ যোগ করলে, ![]() হবে ?
হবে ?
সমাধানঃ
ধরি, ![]() সহিত উহার ‘ ক ‘ অংশ যোগ করলে যোগফল
সহিত উহার ‘ ক ‘ অংশ যোগ করলে যোগফল ![]() হবে
হবে
![]() এর ‘ ক ‘
এর ‘ ক ‘ ![]()
![]() ক ‘
ক ‘ ![]()
![]() (1+ ‘ক ‘ )
(1+ ‘ক ‘ ) ![]()
![]() (1+ ‘ক ‘ )
(1+ ‘ক ‘ ) ![]()
![]() (1+ ‘ক ‘ )
(1+ ‘ক ‘ ) ![]()
![]() (1+ ‘ক ‘ )
(1+ ‘ক ‘ ) ![]()
![]() ‘ক ‘
‘ক ‘ ![]()
![]() এর সহিত উহার
এর সহিত উহার ![]() অংশ যোগ করলে,
অংশ যোগ করলে, ![]() হবে ।
হবে ।
18. ![]() হইতে কত বিয়োগ করিয়া বিয়োগফলকে
হইতে কত বিয়োগ করিয়া বিয়োগফলকে ![]() দিয়া গুন করলে
দিয়া গুন করলে ![]() হবে।
হবে।
সমাধানঃ
![]() – নির্ণেয় সংখ্যা
– নির্ণেয় সংখ্যা ![]()
![]() – নির্ণেয় সংখ্যা
– নির্ণেয় সংখ্যা ![]()
![]() – নির্ণেয় সংখ্যা
– নির্ণেয় সংখ্যা![]()
![]() – নির্ণেয় সংখ্যা
– নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
19. কোন সংখ্যার এক তৃতীয়াংশ হইতে এক পঞ্চমাংশ বিয়োগ করলে 30 হইবে।
সমাধানঃ
নির্ণেয় সংখ্যা ![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যা
নির্ণেয় সংখ্যা ![]()
![]() নির্ণেয় সংখ্যাটি হোল = 225
নির্ণেয় সংখ্যাটি হোল = 225
20. একটি বস্তায় যত আলু ছিল তাহার এক তৃতীয়াংশ তাহার এক দ্বাদশাংশ অপেক্ষা 30 কিলোগ্রাম বেশি। বস্তায় কত আলু ছিল ।
সমাধানঃ
একটি বস্তায় যত আলু ছিল তাহার এক তৃতীয়াংশ ![]() বস্তার মোট আলু এবং
বস্তার মোট আলু এবং
বস্তার আলুর এক দ্বাদশাংশ ![]() বস্তার মোট আলু
বস্তার মোট আলু
প্রশ্নানুসারে, ![]() বস্তার মোট আলু
বস্তার মোট আলু ![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তার মোট আলু =
বস্তার মোট আলু = ![]() কিলোগ্রাম
কিলোগ্রাম
![]() বস্তায় মোট 120 কিলোগ্রাম আলু ছিল ।
বস্তায় মোট 120 কিলোগ্রাম আলু ছিল ।
21. একটি ভগ্নাংশ ![]() অপেক্ষা যত বড়ো
অপেক্ষা যত বড়ো ![]() অপেক্ষা তত ছোটো, ভগ্নাংশ টি নির্ণয় করো ।
অপেক্ষা তত ছোটো, ভগ্নাংশ টি নির্ণয় করো ।
সমাধানঃ
নির্ণেয় ভগ্নাংশ ![]() নির্ণেয় ভগ্নাংশ
নির্ণেয় ভগ্নাংশ
![]() নির্ণেয় ভগ্নাংশ +নির্ণেয় ভগ্নাংশ =
নির্ণেয় ভগ্নাংশ +নির্ণেয় ভগ্নাংশ = ![]()
![]() নির্ণেয় ভগ্নাংশ
নির্ণেয় ভগ্নাংশ ![]()
![]() নির্ণেয় ভগ্নাংশ
নির্ণেয় ভগ্নাংশ ![]()
![]() নির্ণেয় ভগ্নাংশ
নির্ণেয় ভগ্নাংশ ![]()
![]() নির্ণেয় ভগ্নাংশটি হোল =
নির্ণেয় ভগ্নাংশটি হোল = ![]()
22. 168 গজ দৈর্ঘ্য একটি দড়িকে এমন দুই খণ্ডে বিভক্ত করো, যেন একটি খণ্ড অন্যটির ![]() হয় ।
হয় ।
সমাধানঃ
ধরি, দুটি খণ্ডকে একটি কে প্রথম খণ্ড আর অন্যটি কে দ্বিতীয় খণ্ড
![]() দ্বিতীয় খণ্ড =
দ্বিতীয় খণ্ড = ![]() প্রথম খণ্ড
প্রথম খণ্ড
প্রশ্নানুসারে, প্রথম খণ্ড + দ্বিতীয় খণ্ড = 168 গজ
![]() প্রথম খণ্ড +
প্রথম খণ্ড + ![]() প্রথম খণ্ড = 168 গজ
প্রথম খণ্ড = 168 গজ
![]() প্রথম খণ্ড
প্রথম খণ্ড![]() = 168 গজ
= 168 গজ
![]() প্রথম খণ্ড
প্রথম খণ্ড![]() = 168 গজ
= 168 গজ
![]() প্রথম খণ্ড =
প্রথম খণ্ড =![]() গজ
গজ
![]() প্রথম খণ্ড =
প্রথম খণ্ড = ![]() গজ =
গজ = ![]() গজ
গজ ![]() গজ
গজ
![]() দ্বিতীয় খণ্ড টি =
দ্বিতীয় খণ্ড টি = ![]() গজ
গজ
23. দুইটি সংখ্যার যোগফল ![]() , একটি সংখ্যা অন্যটির 3 গুন । সংখ্যা দুইটি নির্ণয় করো ।
, একটি সংখ্যা অন্যটির 3 গুন । সংখ্যা দুইটি নির্ণয় করো ।
সমাধানঃ
দুইটি সংখ্যা কে একটিকে প্রথম সংখ্যা এবং অপরটিকে দ্বিতীয় সংখ্যা ধরিলাম
![]() দ্বিতীয় সংখ্যা =
দ্বিতীয় সংখ্যা = ![]() প্রথম সংখ্যা
প্রথম সংখ্যা
প্রশ্নানুসারে, প্রথম সংখ্যা + দ্বিতীয় সংখ্যা = ![]()
![]() প্রথম সংখ্যা +
প্রথম সংখ্যা +![]() প্রথম সংখ্যা=
প্রথম সংখ্যা= ![]()
![]() প্রথম সংখ্যা =
প্রথম সংখ্যা = ![]()
![]() প্রথম সংখ্যা =
প্রথম সংখ্যা = ![]()
![]() প্রথম সংখ্যা =
প্রথম সংখ্যা = ![]()
![]() দ্বিতীয় সংখ্যা =
দ্বিতীয় সংখ্যা = ![]() প্রথম সংখ্যা=
প্রথম সংখ্যা=![]()
24. একটি বাগানের ![]() অংশের মূল্য 320 টাকা হইলে, সমগ্র বাগানটির মূল্য কত ?
অংশের মূল্য 320 টাকা হইলে, সমগ্র বাগানটির মূল্য কত ?
সমাধানঃ
ধরি বাগান টির সমগ্র অংশ = 1 অংশ
বাগানটির ![]() অংশ = 1 এর
অংশ = 1 এর ![]() অংশ =
অংশ = ![]() অংশ
অংশ
বাগানটির ![]() অংশের মূল্য = 320 টাকা
অংশের মূল্য = 320 টাকা
![]() বাগানটির সমগ্র অংশের মূল্য =
বাগানটির সমগ্র অংশের মূল্য = ![]() টাকা =
টাকা = ![]() টাকা = 768 টাকা
টাকা = 768 টাকা
25. একটি বস্তায়1 কুইন্টাল 25 কিলোগ্রাম চাউল আছে। উহার ![]() অংশের ওজন কত ।
অংশের ওজন কত ।
সমাধানঃ
1 কুইন্টাল 25 কিলোগ্রাম = ![]() কিলোগ্রাম = 125 কিলোগ্রাম
কিলোগ্রাম = 125 কিলোগ্রাম
এক বস্তার চালের ওজন 125 কিলোগ্রাম
উহার ![]() অংশের ওজন =
অংশের ওজন = ![]() কিলোগ্রাম = 75 কিলোগ্রাম
কিলোগ্রাম = 75 কিলোগ্রাম
26. কোন সম্পত্তির ![]() অংশের মূল্য 4340 টাকা হইলে, উহার
অংশের মূল্য 4340 টাকা হইলে, উহার ![]() অংশের মূল্য কত ?
অংশের মূল্য কত ?
সমাধানঃ
ধরি, মোট সম্পত্তির পরিমাণ = 1 অংশ
সম্পত্তির ![]() অংশ = 1 এর
অংশ = 1 এর ![]() অংশ =
অংশ = ![]() অংশ
অংশ
সম্পত্তির ![]() অংশের মূল্য 4340 টাকা
অংশের মূল্য 4340 টাকা
সম্পত্তির 1 অংশ = সমগ্র অংশের মূল্য = ![]() টাকা =
টাকা = ![]() টাকা = 9300
টাকা = 9300
সম্পত্তির ![]() অংশের মূল্য =
অংশের মূল্য = ![]() টাকা = 8137.5 টাকা
টাকা = 8137.5 টাকা
27. কোন সম্পত্তির ![]() এর
এর ![]() অংশ আমি কিনিয়া আমার অংশের
অংশ আমি কিনিয়া আমার অংশের ![]() অংশ 1200 টাকায় বিক্রি করলাম । সমস্ত সম্পত্তির মূল্য কত ?
অংশ 1200 টাকায় বিক্রি করলাম । সমস্ত সম্পত্তির মূল্য কত ?
সমাধানঃ
ধরি, সম্পতির মোট অংশ = 1 অংশ
সম্পত্তির ![]() এর
এর ![]() অংশ
অংশ ![]() অংশ
অংশ ![]() অংশ
অংশ
![]() আমার কেনা সম্পত্তির পরিমাণ =
আমার কেনা সম্পত্তির পরিমাণ = ![]() অংশ
অংশ
আমার সম্পত্তির ![]() অংশ
অংশ ![]() অংশ
অংশ ![]() অংশ
অংশ
![]() সম্পত্তির
সম্পত্তির ![]() অংশের মূল্য = 1200 টাকা
অংশের মূল্য = 1200 টাকা
সম্পত্তির সম্পূর্ণ অংশের মূল্য ![]() টাকা
টাকা ![]() টাকা
টাকা
28. একটি বাঁশের ![]() অংশ কাদায় পোঁতা ছিল,
অংশ কাদায় পোঁতা ছিল, ![]() অংশ জলের ভিতর এবং 6 হাত জলের উপর ছিল । বাঁশটি মোট কত হাত লম্বা ।
অংশ জলের ভিতর এবং 6 হাত জলের উপর ছিল । বাঁশটি মোট কত হাত লম্বা ।
সমাধানঃ
ধরি, বাঁশটির সম্পূর্ণ অংশ = 1 অংশ
![]() বাঁশের
বাঁশের ![]() অংশ কাদায় পোঁতা
অংশ কাদায় পোঁতা ![]() অংশ =
অংশ = ![]() অংশ
অংশ
এবং বাঁশের ![]() অংশ জলের ভিতর =
অংশ জলের ভিতর = ![]() অংশ
অংশ ![]() অংশ
অংশ
![]() কাদায় ও জলের ভিতরে আছে বাঁশের মোট অংশ =
কাদায় ও জলের ভিতরে আছে বাঁশের মোট অংশ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
![]() জলের বাইরে আছে বাঁশের
জলের বাইরে আছে বাঁশের ![]() অংশ =
অংশ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
প্রশ্নানুসারে, ![]() অংশ = 6 হাত লম্বা
অংশ = 6 হাত লম্বা
![]() অংশ =
অংশ = ![]() হাত লম্বা = 20 হাত লম্বা
হাত লম্বা = 20 হাত লম্বা
29. আমার নিকট যত টাকা আছে তাহার ![]() অংশ ‘ক’ কে,
অংশ ‘ক’ কে, ![]() অংশ ‘খ’ কে এবং অবশিষ্ট 36 টাকা ‘গ’ কে দিলাম । আমার নিকট কত টাকা ছিল এবং কে কত টাকা পাইল ।
অংশ ‘খ’ কে এবং অবশিষ্ট 36 টাকা ‘গ’ কে দিলাম । আমার নিকট কত টাকা ছিল এবং কে কত টাকা পাইল ।
সমাধানঃ
ধরি, আমার নিকট টাকার পরিমাণ = 1 অংশ
‘ক ‘ কে দেওয়া টাকার পরিমাণ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
‘খ ‘ কে দেওয়া টাকার পরিমাণ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
‘ক ‘ ও ‘খ ‘ কে দেওয়া মোট টাকার পরিমাণ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
‘ক ‘ ও ‘খ ‘ কে দেওয়ার পর আমার কাছে থাকা অবশিষ্ট টাকার পরিমাণ = ![]() অংশ=
অংশ= ![]() অংশ =
অংশ = ![]() অংশ
অংশ
প্রশ্নানুসারে, ![]() অংশ = 36 টাকা
অংশ = 36 টাকা
![]() 1 অংশ =
1 অংশ = ![]() টাকা = 64 টাকা
টাকা = 64 টাকা
![]() আমার নিকট মোট টাকার পরিমাণ = 64 টাকা
আমার নিকট মোট টাকার পরিমাণ = 64 টাকা
‘ক ‘ এর প্রাপ্ত টাকার পরিমাণ = ![]() টাকা = 12 টাকা এবং
টাকা = 12 টাকা এবং
‘খ’ এর প্রাপ্ত টাকার পরিমাণ = ![]() টাকা = 16 টাকা
টাকা = 16 টাকা
30. একটি সৈন্যদলে মোট যত সৈন্য ছিল তাহার ![]() অংশ অসুখে মারা গেল,
অংশ অসুখে মারা গেল, ![]() অংশ যুদ্ধ মারা গেল এবং অবশিষ্ট 22600 জন সৈন্য পালিয়ে গেল । সেই দলে মোট কত সৈন্য ছিল ।
অংশ যুদ্ধ মারা গেল এবং অবশিষ্ট 22600 জন সৈন্য পালিয়ে গেল । সেই দলে মোট কত সৈন্য ছিল ।
সমাধানঃ
ধরি, সৈন্যদলে মোট সৈন্যের সংখ্যা = 1 অংশ
অসুখে মারা যাওয়া সৈন্যের সংখ্যা = ![]() অংশ=
অংশ= ![]() অংশ
অংশ
যুদ্ধ-এ মারা যাওয়া সৈন্যের সংখ্যা = ![]() অংশ=
অংশ= ![]() অংশ
অংশ
![]() অসুখে ও যুদ্ধ-এ মারা যাওয়া মোট সৈন্যের সংখ্যা =
অসুখে ও যুদ্ধ-এ মারা যাওয়া মোট সৈন্যের সংখ্যা = ![]() অংশ =
অংশ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
![]() অসুখে ও যুদ্ধ-এ মারা যাওয়ার পর অবশিষ্ট থাকা মোট সৈন্যের সংখ্যা =
অসুখে ও যুদ্ধ-এ মারা যাওয়ার পর অবশিষ্ট থাকা মোট সৈন্যের সংখ্যা = ![]() অংশ =
অংশ = ![]() অংশ =
অংশ = ![]() অংশ
অংশ
প্রশ্নানুসারে, ![]() অংশ = 22600 জন
অংশ = 22600 জন
![]() অংশ =
অংশ = ![]() জন =
জন = ![]() জন= 33000 জন
জন= 33000 জন
![]() সেই সৈন্যদলে মোট 33000 সৈন্য ছিল ।
সেই সৈন্যদলে মোট 33000 সৈন্য ছিল ।
এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।
