শ্রেণী সপ্তম
কষে দেখি -12.2
বীজগাণিতিক সূত্রাবলী
………………………………………………………………………………………………..
1. ![]() এই অভেদের সাহায্যে নিচের বীজগাণিতিক সংখ্যামালা গুলি গুন করি ।
এই অভেদের সাহায্যে নিচের বীজগাণিতিক সংখ্যামালা গুলি গুন করি ।
![]()
সমাধানঃ

![]()
সমাধানঃ
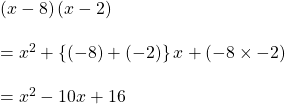
![]()
সমাধানঃ

![]()
সমাধানঃ

![]()
সমাধানঃ
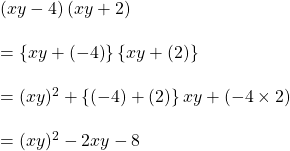
![]()
সমাধানঃ

2. সূত্রের সাহায্যে দেখাই যে —
![]()
সমাধানঃ
বাম পক্ষ

ডান পক্ষ
![]()
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
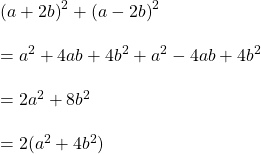
ডান পক্ষ
![]()
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
![]()
ডান পক্ষ

![]()
সমাধানঃ
বাম পক্ষ
![]()
ডান পক্ষ

![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
![]()
ডান পক্ষ
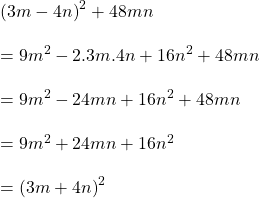
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
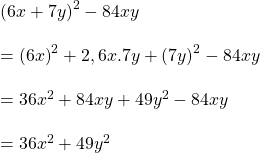
ডান পক্ষ
![]()
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
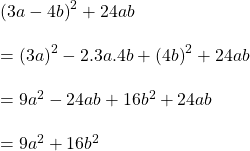
ডান পক্ষ
![]()
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
![]()
সমাধানঃ
বাম পক্ষ
![]()
ডান পক্ষ
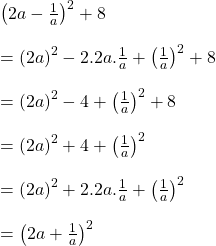
![]() বাম পক্ষ =ডান পক্ষ
বাম পক্ষ =ডান পক্ষ
3. প্রতিক্ষেত্রে সূত্রের সাহায্যে সমস্যা সমাধান করি
![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
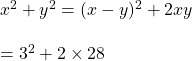
![]() মান বসিয়ে পাই
মান বসিয়ে পাই
![]()
![]() হলে,
হলে, ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ

![]() মান বসিয়ে পাই
মান বসিয়ে পাই
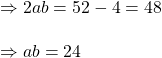
![]() এবং
এবং ![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
আমরা জানি যে,

![]()
![]() এবং
এবং ![]() মান বসিয়ে পাই
মান বসিয়ে পাই

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,
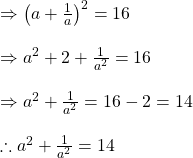
![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে দেখাই যে
হলে দেখাই যে ![]()
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে প্রমাণ করি যে
হলে প্রমাণ করি যে ![]()
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

(প্রমাণিত )
![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
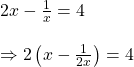
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,
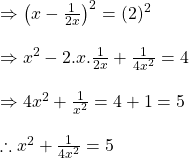
![]() হলে দেখাই যে
হলে দেখাই যে ![]()
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,
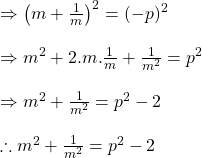
![]() হলে দেখাই যে
হলে দেখাই যে ![]()
সমাধানঃ
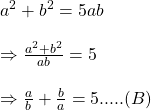
![]() -এর উভয়পক্ষকে বর্গকরে পাই,
-এর উভয়পক্ষকে বর্গকরে পাই,
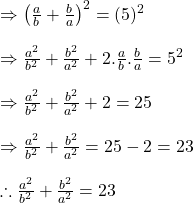
![]() হলে দেখাই যে
হলে দেখাই যে ![]()
সমাধানঃ

![]() -এর উভয়পক্ষকে বর্গকরে পাই
-এর উভয়পক্ষকে বর্গকরে পাই
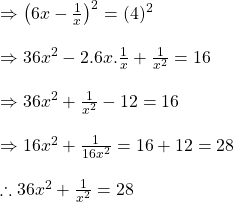
![]() হলে দেখাই যে
হলে দেখাই যে ![]()
সমাধানঃ
![]() উভয়পক্ষকে বর্গকরে পাই,
উভয়পক্ষকে বর্গকরে পাই,

![]() হলে
হলে ![]() এর মান কত লিখি ।
এর মান কত লিখি ।
সমাধানঃ
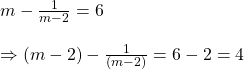
![]()
![]() -এর উভয়পক্ষকে বর্গকরে পাই
-এর উভয়পক্ষকে বর্গকরে পাই

এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।

