………………………………………………………………………..
Class-VIII
প্রশ্নমালা -6.2
K. C. NAG
………………………………………………………………………..
সমষ্টি নির্ণয় করোঃ
সমষ্টি নির্ণয় করোঃ
(i). ![]()
সমাধানঃ
![]() এদের সমষ্টি
এদের সমষ্টি

(ii). ![]()
সমাধানঃ
![]() এদের সমষ্টি
এদের সমষ্টি

(iii). ![]()
সমাধানঃ
![]() এদের সমষ্টি
এদের সমষ্টি

(iv). ![]()
সমাধানঃ
![]() এদের সমষ্টি
এদের সমষ্টি

(v). ![]()
সমাধানঃ
![]() এদের সমষ্টি
এদের সমষ্টি

সরল করোঃ
1. ![]()
সমাধানঃ

2. 
সমাধানঃ

3. 
সমাধানঃ

4. 
সমাধানঃ

5. 
সমাধানঃ

6. 
সমাধানঃ

7. 
সমাধানঃ

8. 
সমাধানঃ

9. 
সমাধানঃ

10. 
সমাধানঃ

11. 
সমাধানঃ

12. 
সমাধানঃ

13. 
সমাধানঃ

14. 
সমাধানঃ

15. ![]()
সমাধানঃ
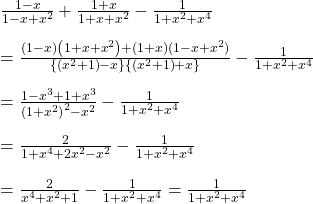
16. ![]()
সমাধানঃ

17. ![]()
সমাধানঃ

18. ![]()
সমাধানঃ

19. 
সমাধানঃ

20. ![]()
সমাধানঃ

Share this Post
এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।

