Annual Examination—2021
MODEL QUESTIONSOLVED-দাগ নাম্বার – A& B
Class — VII
Subject : Mathematics
………………………………………………………………………………………………………………………………………………….
সমাধানঃ
সমাধানঃ
সমাধানঃ
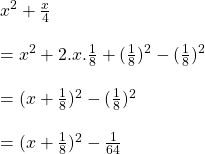

সমাধানঃ
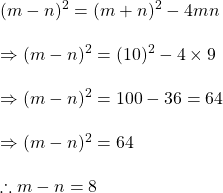

সমাধানঃ
অতিক্রান্ত দূরত্ব = গতিবেগ 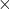 প্রয়োজনীয় সময়
প্রয়োজনীয় সময়

সমাধানঃ
1 মিটার = 100 সেন্টিমিটার
1 সেন্টিমিটার = 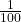 মিটার
মিটার
1 বর্গসেন্টিমিটার = 1 সেন্টিমিটার 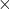 1 সেন্টিমিটার
1 সেন্টিমিটার
= 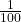 মিটার
মিটার 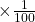 মিটার
মিটার
= 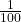
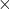
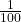 বর্গ মিটার
বর্গ মিটার
= 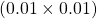 বর্গ মিটার
বর্গ মিটার
= 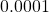 বর্গ মিটার
বর্গ মিটার

সমাধানঃ


সমাধানঃ

সমাধানঃ
Option: (a)


সমাধানঃ
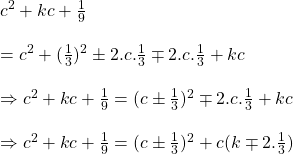
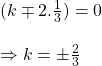
সমাধানঃ
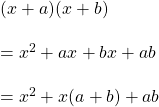
সমাধানঃ
সমাধানঃ

সমাধানঃ
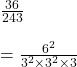
এই 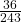 সংখ্যাটি পূর্ণবর্গ নয় কারণ 243 =
সংখ্যাটি পূর্ণবর্গ নয় কারণ 243 = 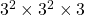 এখানে একটি 3 অযুগ্ম বার আছে,
এখানে একটি 3 অযুগ্ম বার আছে,
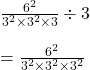

সমাধানঃ

সমাধানঃ


সমাধানঃ
একক সময়ে কোনো বস্তূ নির্দিষ্ট দিকে যতটা দূরত্ব অতিক্রম করে সেটাই ওই বস্তুর গতিবেগ.
![]()
সমাধানঃ
দুটি স্তম্ভ চিত্র পাশাপাশি এঁকে দুটি তথ্য সহজে তুলনা করার জন্য যে চিত্র আঁকা হয় তাকে দ্বি-স্তম্ভ লেখ বলে ।


সমাধানঃ
একটি আয়তক্ষেত্রাকার ঘরের দৈর্ঘ্য = 30 মিটার
আয়তক্ষেত্রাকার ঘরের প্রস্থ = 18 মিটার
আয়তক্ষেত্রাকার ঘরের মেঝের ক্ষেত্রফল = 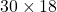 বর্গমিটার =
বর্গমিটার = 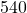 বর্গমিটার
বর্গমিটার
বর্গাকার টালির বাহুর দৈর্ঘ্য = 3 ডেসিমিটার= 0.3 মিটার
বর্গাকার টালির ক্ষেত্রফল = 0.09 বর্গমিটার
ঘরটির মেঝে বাঁধাতে মোট = 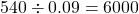 টালি লাগবে
টালি লাগবে
![]()
সমাধানঃ
ঘূর্ণন কেন্দ্রের সাপেক্ষে কোন বস্তুর সম্পূর্ণ একবার ঘুরে আসতে অর্থাৎ 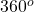 কোন ঘুরতে যতবার প্রথম অবস্থার সাথে সম্পূর্ণভাবে মিলে যায় তাকে ঘূর্ণন প্রতিসাম্য মাত্রা বলে ।
কোন ঘুরতে যতবার প্রথম অবস্থার সাথে সম্পূর্ণভাবে মিলে যায় তাকে ঘূর্ণন প্রতিসাম্য মাত্রা বলে ।
![]()
সমাধানঃ
সামান্তরিকের ঘূর্ণন প্রতিসাম্য কোন 
![]()
সমাধানঃ
সুষম ষড়ভুজের ঘূর্ণন প্রতিসাম্য মাত্রা 6 টি
![]()
সমাধানঃ
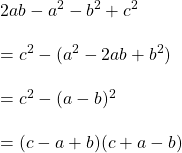
![]()
সমাধানঃ
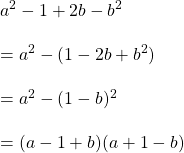
![]()
সমাধানঃ
(আরও সমাধান হতে পারে )
![]()
সমাধানঃ
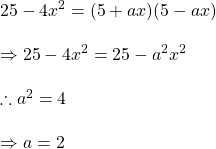
এই ব্লগ সাইটটির আরও উন্নতির জন্যে সকলের কাছে থেকে যেকোনো ধরনের পরামর্শ সাদরে গ্রহন করা হবে।









Sir CLASS 7 AR B AR DAGER 6 NUMBER AR TAR ANSWER 600 TALI HOBE . APNI 6000 LIKHE6EN .