Solution of sample questions -VIII/অষ্টম শ্রেণী /দাগ নম্বর-5
5. প্রতিটি প্রশ্নের উত্তর দাও [প্রশ্নমান ৩]
i. উৎপাদক বিশ্লেষণ করো :
a). 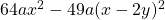
উত্তরঃ
![Rendered by QuickLaTeX.com 64ax^{2}-49a(x-2y)^{2}\\\\=a\left [ \left ( 8x \right )^{2}- \left \{ 7\left ( x-2y \right ) \right \}^{2} \right ]\\\\=a\left [ \left ( 8x \right )^{2}-\left ( 7x-14y \right )^{2}\right ]\\\\=a\left \{ 8x-\left ( 7x-14y \right ) \right \}\left \{ 8x+\left ( 7x-14y \right ) \right \}\\\\=a\left \{ 8x- 7x+14y \right \}\left \{ 8x+ 7x-14y \right \}\\\\=a\left ( x+14y \right )\left ( 15x-14y \right )](https://sdtutoronline.com/wp-content/ql-cache/quicklatex.com-0d7f827b65313377691e5af23902e74c_l3.png)
b). 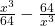
উত্তরঃ
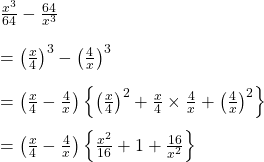
c). 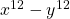
উত্তরঃ
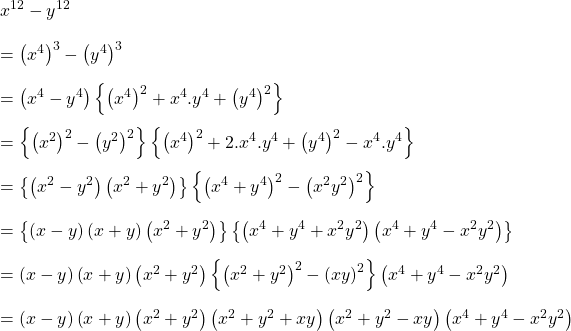
d).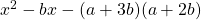
উত্তরঃ
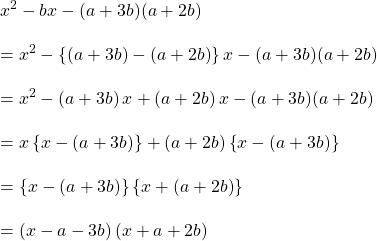
e).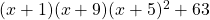
উত্তরঃ
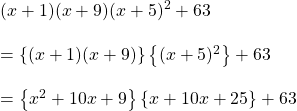 ধরি,
ধরি, ![]()
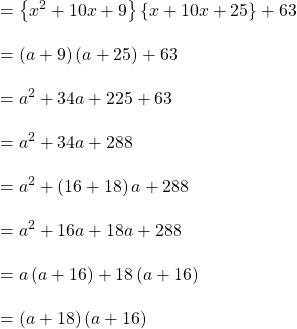
![]() এর মান বসিয়ে পাই,
এর মান বসিয়ে পাই, 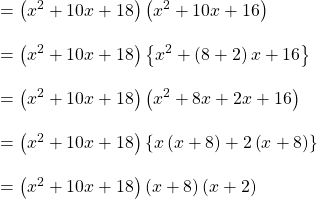
f).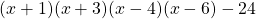
উত্তরঃ
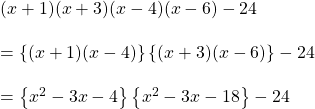
ধরি, ![]()
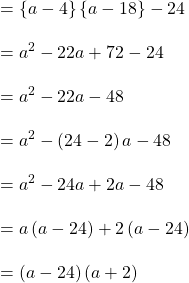
![]()
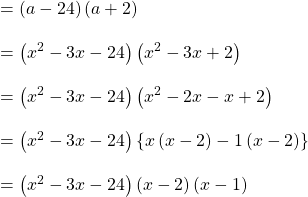
ii. ধারাবাহিক গুন করো
a). 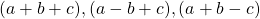
উত্তরঃ
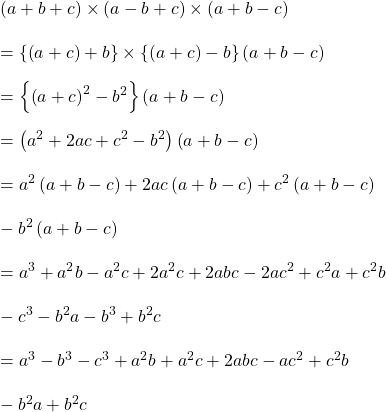
b). 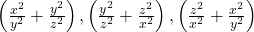
উত্তরঃ
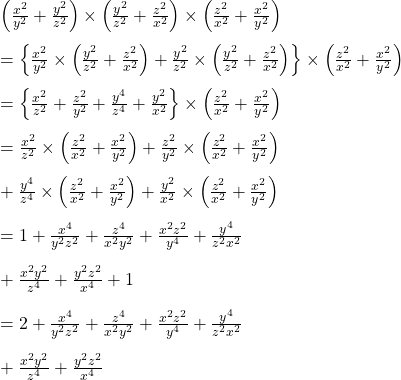
iii. 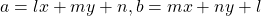 এবং
এবং 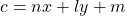 হলে,
হলে, 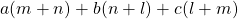 এর মান নির্ণয় করো।
এর মান নির্ণয় করো।
উত্তরঃ
![]()
![]() এবং
এবং ![]()
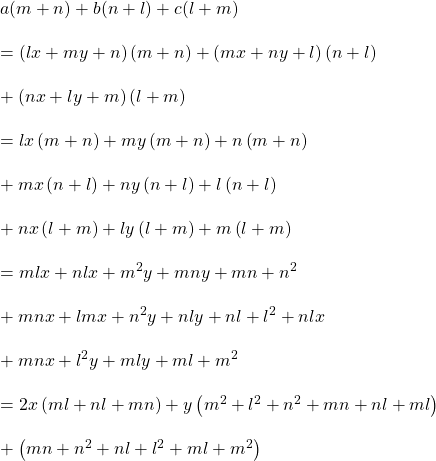
iv. ভাগ করো : 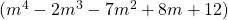 কে
কে 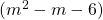 দিয়ে।
দিয়ে।
উত্তরঃ

v). 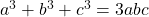 হলে,
হলে, 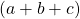 এর মান নির্ণয় করো। [
এর মান নির্ণয় করো। [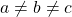 ]
]
উত্তরঃ
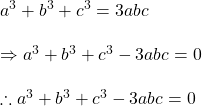
![]()
![]()
![]()
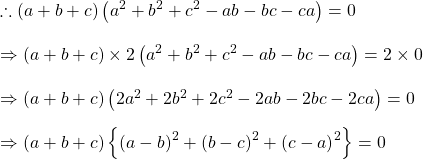
![]() এবং
এবং ![]() এর গুনফল
এর গুনফল ![]()
হয়, ![]() অর্থবা,
অর্থবা, ![]()
কিন্তু ![]()
কারণ, ![]() ,
, ![]() এবং
এবং ![]() যদি
যদি ![]() তাহলে
তাহলে 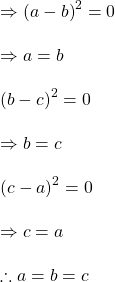 ,কিন্তু
,কিন্তু ![]()
![]()
vi). সরল করো :
a). 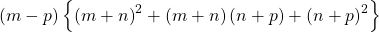
উত্তরঃ
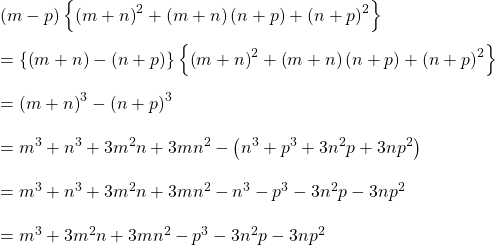
b).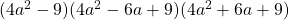
উত্তরঃ
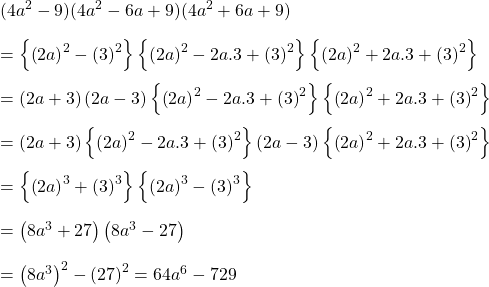
c). 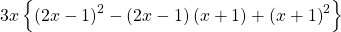
উত্তরঃ
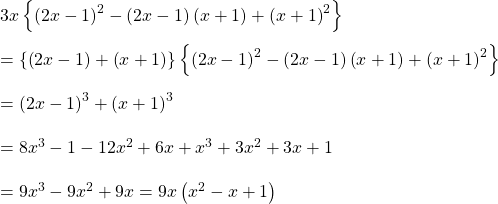
vii). 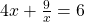 হলে,
হলে, 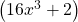 এর মান নির্ণয় করো।
এর মান নির্ণয় করো।
উত্তরঃ
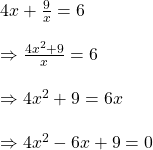
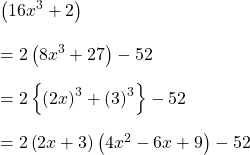
![]() এর মান বসিয়ে পাই,
এর মান বসিয়ে পাই, 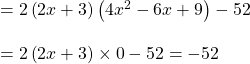
![]()
viii). 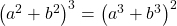 হলে,
হলে, 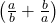 এর মান নির্ণয় করো।
এর মান নির্ণয় করো।
উত্তরঃ
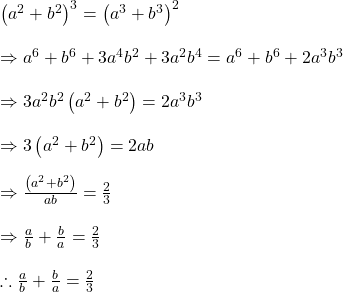
ix). 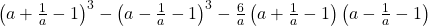
উত্তরঃ
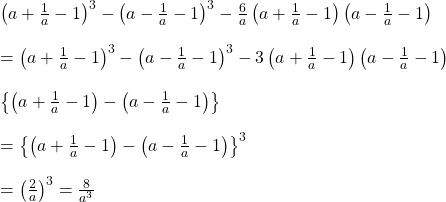
x. একটি ঘনকের আয়তন 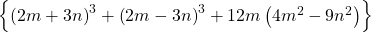 ঘন একক হলে, ঘনকের একটি বাহুর দৈর্ঘ্য নির্ণয় করো।
ঘন একক হলে, ঘনকের একটি বাহুর দৈর্ঘ্য নির্ণয় করো।
উত্তরঃ
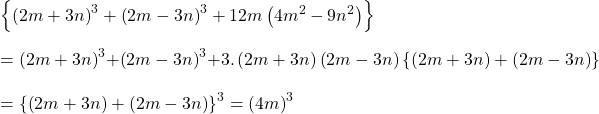
![]() ঘনকের একটি বাহুর দৈর্ঘ্য
ঘনকের একটি বাহুর দৈর্ঘ্য ![]() একক।
একক।
CLASS-VIII-দাগ নাম্বার -3 -Annual Examination—2021/MODEL QUESTION SOLVED/Mathematics:
http://sdtutoronline.com/class-8-importat-wbmath-suggestion/
Class-VIII-দাগ নাম্বার-1&2,Annual:
http://sdtutoronline.com/class-viii-model-math-question-wb/
Class -VIII/ Model activity task / বহু বিকল্পভিত্তিক প্রশ্নঃ পরিচিতি ও অনুশীলনী গণিত/ অষ্টম শ্রেণী:
http://sdtutoronline.com/wb-class-viii-model-activity-task-math-8/
