অষ্টম শ্রেণী
Solution of sample questions -VIII/অষ্টম শ্রেণী /দাগ নম্বর -3
3. প্রতিটি প্রশ্নের উত্তর দাও [প্রশ্নমান -২]
i. যোগের বিনিময় সংযোগ নিয়ম ব্যবহার করে মান নির্ণয় করো।
![]()
উত্তরঃ
![Rendered by QuickLaTeX.com \frac{5}{8}+(-\frac{7}{15})+\frac{3}{32}+\frac{11}{75}\\\\=\frac{5}{8}+[(-\frac{7}{15})+\frac{3}{32}]+\frac{11}{75}\\\\=\frac{5}{8}+[\frac{3}{32}+(-\frac{7}{15})]+\frac{11}{75}\\\\=[\frac{5}{8}+\frac{3}{32}]+[(-\frac{7}{15})+\frac{11}{75}]\\\\=[\frac{20+3}{32}]+[\frac{-35+11}{75}]\\\\=\frac{23}{32}+(\frac{-24}{75})\\\\=\frac{23\times 75-24\times 32}{32\times 75}=\frac{957}{2400}=\frac{319}{800}](https://sdtutoronline.com/wp-content/ql-cache/quicklatex.com-20796078d6eb6f2b31e672f8bbb99668_l3.png)
ii. গুনের বিনিময় ও সংযোগ নিয়ম ব্যবহার করে মান নির্ণয় করো
![]()
উত্তরঃ

iii. 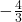 ও
ও  এর মধ্যে 5 টি মূলদ সংখ্যা নির্ণয় করো
এর মধ্যে 5 টি মূলদ সংখ্যা নির্ণয় করো
উত্তরঃ
ধরি, 
![]()
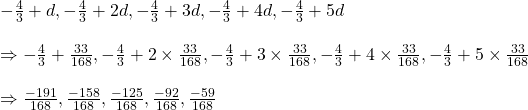
এই মূলদ সংখ্যা গুলির বিশেষ বৈশিষ্ট হলো এরা সমদূরবর্তী।
iv. গল্প তৈরী করো ও ত্রৈরাশিক পদ্ধতিতে সমাধান করো :
গতিবেগ (কিমি /ঘন্টা ) দূরত্ব (কিমি )
9 112.5 12 ?
উত্তরঃ
গল্প : রতন বাবু তাঁর বাইসাইকেল করে 9কিমি/ঘন্টা গতিবেগে কিছু সময়ে তিনি 112.5 কিমি দূরত্ব যায়।
যদি সে তার সাইকেলের পরিবর্তে তাঁর মোটরসাইকেলে যেত তাহলে তিনি কত দূরত্ব অতিক্রম করতো
ওই একেই সময়ে , যদি তার মোটর সাইকেলের গতিবেগ 12 কিমি /ঘন্টা হয় ।
সমাধানঃ
গতিবেগ বাড়লে নির্দিষ্টি সময়ে বেশি দূরত্ব অতিক্রম করবে, আর গতিবেগ কমলে নির্দিষ্টি সময়ে কম
দূরত্ব অতিক্রম করবে,![]() গতিবেগের অনুপাতের সঙ্গে অতিক্রান্ত দূরত্বের অনুপাত সরলসমানুপাতে আছে
গতিবেগের অনুপাতের সঙ্গে অতিক্রান্ত দূরত্বের অনুপাত সরলসমানুপাতে আছে ![]() নির্ণেয় অতিক্রান্ত দূরত্ব
নির্ণেয় অতিক্রান্ত দূরত্ব 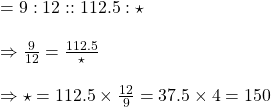
![]()
v. জল জমে বরফ হলে আয়তন 10% বৃদ্ধি পায়। এই বরফ গলে জল হলে
আয়তন শতকরা কত হ্রাস পাবে ?
উত্তরঃ
ধরি, ![]() ঘন একক জল জমে বরফে পরিণত হলো
ঘন একক জল জমে বরফে পরিণত হলো ![]() ঘন একক জল জমে বরফে পরিণত হলে বরফের আয়তন হবে
ঘন একক জল জমে বরফে পরিণত হলে বরফের আয়তন হবে
![]() ঘন একক
ঘন একক ![]() ঘন একক
ঘন একক ![]()
ওই
শতকরা হ্রাস

vi. চিনির মূল্য 20% বেড়ে গেছে। তাই চিনির মাসিক খরচ অপরিবর্তিত
রাখতে চিনির মাসিক ব্যবহারের পরিমান শতকরা কত কম করতে হবে ?
উত্তরঃ
ধরি, আগে মাসে ![]() টাকা খরচ হতো
টাকা খরচ হতো ![]() একক চিনির জন্যে
একক চিনির জন্যে
এখন, 20% চিনির মূল্য বেড়ে যাওয়াতে ওই ![]() একক চিনির মূল্য হবে
একক চিনির মূল্য হবে
=![]() টাকা =
টাকা =![]() টাকা =
টাকা =![]() টাকা
টাকা
কিন্তু খরচ অপরিবর্তত রাখতে ওই ![]() টাকায় এখন কত চিনি পাওয়া যাবে,
টাকায় এখন কত চিনি পাওয়া যাবে,
এখন, ![]() টাকায় পাওয়া যায়
টাকায় পাওয়া যায় ![]() একক চিনি ,, 1 ,, ,,
একক চিনি ,, 1 ,, ,, ![]() একক চিনি ,,
একক চিনি ,, ![]() ,, ,,
,, ,, ![]() একক চিনি
একক চিনি
![]() চিনির পরিমানের মাসিক ব্যবহার কমবে =
চিনির পরিমানের মাসিক ব্যবহার কমবে = ![]() একক
একক
![]() চিনির ব্যবহারের শতকরা পরিমান কমবে
চিনির ব্যবহারের শতকরা পরিমান কমবে 
![]() চিনির মাসিক খরচ অপরিবর্তিত রাখতে চিনির মাসিক ব্যবহারের পরিমান শতকরা
চিনির মাসিক খরচ অপরিবর্তিত রাখতে চিনির মাসিক ব্যবহারের পরিমান শতকরা ![]() কম করতে হবে
কম করতে হবে
vii. t- এর কোন মানের জন্য  একটি পূর্ণবর্গ সংখ্যামালা
একটি পূর্ণবর্গ সংখ্যামালা
হবে?
উত্তরঃ

![]() পূর্নবর্গ হবে যদি
পূর্নবর্গ হবে যদি ![]() হয় ,
হয় , 
![]() হলে
হলে ![]() একটি পূর্ণবর্গ সংখ্যামালা হবে।
একটি পূর্ণবর্গ সংখ্যামালা হবে।
viii. দুটি বর্গের অন্তররূপে প্রকাশ করো : 
উত্তরঃ

ix.  হলে
হলে 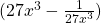 এর মান কত হবে?
এর মান কত হবে?
উত্তরঃ
![]()
(i) নম্বরের উভয়পক্ষকে 3 দিন গুন করে পাই , ![]()
(iii) নং এর উভয়পক্ষকে ঘন করে পাই,
![]()
x.  হলে
হলে  এর মান নির্ণয় করো।
এর মান নির্ণয় করো।
উত্তরঃ
![]()
(i) নং এর উভয়পক্ষকে ঘন করে পাই, 
![]()
xi. 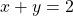 এবং
এবং  হলে
হলে  এর মান
এর মান
নির্ণয় করো।
উত্তরঃ
![]() এবং
এবং 
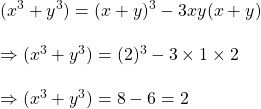
![]()
xii. ঘন নির্ণয় করো : 
উত্তরঃ
![]()
ঘন করে পাই, 
xiii.  এর উৎপাদক গুলির সমষ্টি কত হবে ?
এর উৎপাদক গুলির সমষ্টি কত হবে ?
উত্তরঃ

উৎপাদক গুলির সমষ্টি হলো : ![]()
xiv. সরল করো :
উত্তরঃ

xv.  হলে
হলে  এর মান কত ?
এর মান কত ?
উত্তরঃ
![]()
(i) নং এর উভয়পক্ষকে বর্গ করে পাই, 
![]()
(i) নং এর উভয়পক্ষকে ঘন করে পাই, 
![]()
![]() নং ও
নং ও ![]() নং কে গুন করে পাই,
নং কে গুন করে পাই, 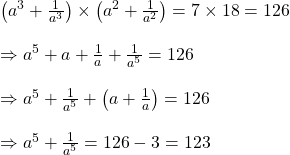
![]()
xvi.  হলে
হলে 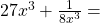 কত হবে ?
কত হবে ?
উত্তরঃ
![]()
![]() এর উভয়পক্ষকে
এর উভয়পক্ষকে ![]() দিয়ে গুন করে পাই,
দিয়ে গুন করে পাই, 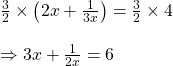
![]()
![]() নং এর উভয়পক্ষকে ঘন করে পাই,
নং এর উভয়পক্ষকে ঘন করে পাই, 
![]()
xvii. কোনো কোনের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক এর মধ্যবর্তী
কোনের মান নির্ণয় করো।
উত্তরঃ

![]() এর অন্তঃসমদ্বিখণ্ডক
এর অন্তঃসমদ্বিখণ্ডক ![]() এবং বহিঃসমদ্বিখণ্ডক হলো
এবং বহিঃসমদ্বিখণ্ডক হলো ![]()
![]() (অন্তঃকোন ও বহিঃকোনের যোগফল সর্বদা
(অন্তঃকোন ও বহিঃকোনের যোগফল সর্বদা ![]() )
)
![]() কোনো কোনের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক এর মধ্যবর্তী কোনের মান
কোনো কোনের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক এর মধ্যবর্তী কোনের মান ![]() .
.
xviii. 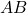 সরলরেখাংশের
সরলরেখাংশের  ও
ও  বিন্দুতে
বিন্দুতে 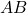 সরলরেখাংশের বিপরীত
সরলরেখাংশের বিপরীত
পাশে  ও
ও  দুটি সমান কোনের সমদ্বিখণ্ডক দুটি
দুটি সমান কোনের সমদ্বিখণ্ডক দুটি
কিভাবে অবস্থিত তা নির্ণয় করো ?
উত্তরঃ

যেহেতু ![]() ,
, ![]()
![]() ও
ও ![]() সমদ্বিখন্ডকের ফলে উৎপন্ন কোনদুটিও সমান হবে,
সমদ্বিখন্ডকের ফলে উৎপন্ন কোনদুটিও সমান হবে, ![]()
![]() ও
ও ![]() দুটি সরল রেখা এবং
দুটি সরল রেখা এবং ![]() ছেদক এর ফলে উৎপন্ন একান্তর কোন
ছেদক এর ফলে উৎপন্ন একান্তর কোন ![]() ও
ও ![]() আবার,
আবার, ![]()
![]()
xix. একটি স্থুলকোনী সমদ্বিবাহু ত্রিভুজের সূক্ষকোণের পরিমাপ স্থুলকোনের
পরিমাপের  অংশ হলে ত্রিভুজটির প্রত্যেক কোনের পরিমাপ
অংশ হলে ত্রিভুজটির প্রত্যেক কোনের পরিমাপ
করো।
উত্তরঃ

ধরি , ![]() একটি স্থুলকোনী সমদ্বিবাহু ত্রিভুজ যার
একটি স্থুলকোনী সমদ্বিবাহু ত্রিভুজ যার ![]() এবং
এবং ![]() হলো একটি স্থুলকোন,
হলো একটি স্থুলকোন,
যেহেতু, ![]()
![]()
ধরি, ![]()
প্রশ্নানুসারে, ![]()

![]() এবং
এবং ![]()
xx. দেখাও যে একটি সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু দিয়ে ভূমির সমান্তরাল
সরলরেখা শীর্ষ কোনের বহিঃ সমদ্বিখণ্ডক।
উত্তরঃ

প্রদত্ত : ![]() এর
এর ![]() এবং
এবং ![]()
প্রামাণ্য : ![]() অর্থাৎ
অর্থাৎ ![]() শীর্ষকোন
শীর্ষকোন ![]() এর বহিঃসমদ্বিখণ্ডক।
এর বহিঃসমদ্বিখণ্ডক।
প্রমান : ![]() এর
এর ![]() সুতরাং,
সুতরাং, ![]()
![]() এবং
এবং ![]() ছেদক। সুতরাং
ছেদক। সুতরাং ![]() (একান্তরকোন )
(একান্তরকোন )![]() এবং
এবং ![]() ছেদক। সুতরাং
ছেদক। সুতরাং ![]() (অনুরূপকোন )
(অনুরূপকোন )
যেহেতু, ![]() , সুতরাং
, সুতরাং ![]() (প্রমাণিত )
(প্রমাণিত )
Solution of sample questions – VIII / অষ্টম শ্রেণী / দাগ নম্বর 2:
http://sdtutoronline.com/solution-of-sample-questions-viii-2-2/

